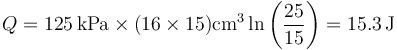Test del Examen Parcial 2014-2015

De Laplace

Contenido

1 Campo con simetría esférica
2 Dos cargas en el plano
3 Separación de las placas de un condensador
- 3.1 Pregunta 1
- 3.2 Pregunta 3
4 Afirmaciones sobre un conductor
5 Dos cargas en una varilla
6 Vuelco de un cilindro
- 6.1 Pregunta 1
- 6.2 Pregunta 2

1 Campo con simetría esférica

El campo eléctrico generado por una cierta distribución tiene la expresión

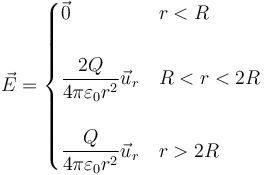
$\vec{E}=\begin{cases}\vec{0} & r < R \\ & \\ \displaystyle\frac{2Q}{4\pi\varepsilon_0 r^2}\vec{u}_r & R < r < 2R \\ & \\ \displaystyle\frac{Q}{4\pi\varepsilon_0 r^2}\vec{u}_r & r>2R\end{cases}$

1.1 Pregunta 1

¿Cómo es la distribución de carga que crea este campo?

A Solo una superficie esférica de carga $+ Q$ en $r = 2 R$ .
B Una superficie esférica de carga $+ 2 Q$ en $r = R$ y una de carga $- Q$ en $r = 2 R$ .
C Solo una superficie esférica de carga $+ 2 Q$ en $r = R$ .
D Una superficie esférica de carga $+ 2 Q$ en $r = R$ y una de carga $+ Q$ en $r = 2 R$ .

Solución

La respuesta correcta es la B.

De acuerdo con la ley de Gauss, el flujo del campo eléctrico a través de una superficie cerrada es igual a la carga encerrada por ella.

Para este campo, en $r < R$ no hay carga. Entre $R$ y $2 R$ tenemos el campo de una carga $2 Q$ , por tanto, esta es la carga en la superficie $r = R$ .

A partir de $r = 2 R$ vemos el campo de una carga Q. Por tanto, esta es la carga encerrada por una superficie de $r > 2 R$ . Pero esta carga incluye la carga $2 Q$ que está en $r = R$ . Por tanto, la carga que hay en la superficie $r = 2 R$ vale $- Q$

1.2 Pregunta 2

¿Cuanto vale el potencial eléctrico en $r = 0$ , tomando como origen de potencial el infinito?

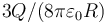
A $3Q/(8\pi\varepsilon_0 R)$
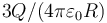
B $3Q/(4\pi\varepsilon_0 R)$
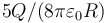
C $5Q/(8\pi\varepsilon_0 R)$
D $0$

Solución

La respuesta correcta es la A.

Puede hallarse por superposición o integrando el campo eléctrico.

Por superposición sería la suma del potencial en el interior de una esfera de carga $2 Q$ en $r = R$ y de una de carga $- Q$ en $r = 2 R$

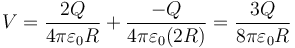
$V = \frac{2Q}{4\pi\varepsilon_0 R}+\frac{-Q}{4\pi\varepsilon_0(2R)}=\frac{3Q}{8\pi\varepsilon_0 R}$

Por integración del campo sería la suma de tres tramos

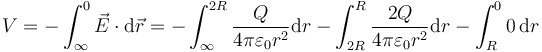
$V = -\int_\infty^0\vec{E}\cdot\mathrm{d}\vec{r}=-\int_\infty^{2R}\frac{Q}{4\pi\varepsilon_0 r^2}\mathrm{d}r-\int_{2R}^R\frac{2Q}{4\pi\varepsilon_0 r^2}\mathrm{d}r-\int_{R}^00\,\mathrm{d}r$

y da

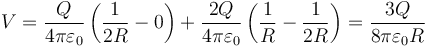
$V = \frac{Q}{4\pi\varepsilon_0}\left(\frac{1}{2R}-0\right)+\frac{2Q}{4\pi\varepsilon_0}\left(\frac{1}{R}-\frac{1}{2R}\right)=\frac{3Q}{8\pi\varepsilon_0R}$

1.3 Pregunta 3

¿Cuánta energía almacena la distribución?

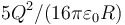
A $5Q^2/(16\pi\varepsilon_0 R)$
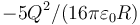
B $-5Q^2/(16\pi\varepsilon_0 R)$
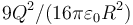
C $9Q^2/(16\pi\varepsilon_0 R^2)$
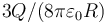
D $3Q/(8\pi\varepsilon_0 R)$

Solución

La respuesta correcta es la A.

Esta energía puede calcularse de diferentes formas.

Una es observar que no todas las opciones son iguales dimensionalmente. Una energía electrostática tiene unidades de carga por potencial, por tanto debe ser de la forma

$U_e = \alpha (Q)\left(\frac{Q}{4\pi\varepsilon_0 R}\right)= \alpha \frac{Q^2}{4\pi\varepsilon_0 R}$

siendo $α$ un número (sin unidades) que dependerá de cada problema concreto.

Eso nos hace descartar las opciones C (hay un R² en el denominador) y D (falta el cuadrado de la carga).

Por otro parte, la energía de una distribución de carga superficial o volumétrica es siempre positiva. Esto descarta la B. Por tanto, la respuesta correcta es la A.

No obstante, también se puede hallar por cálculo de distintas formas. Una es a partir de la energía de esferas concéntricas

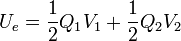
$U_e = \frac{1}{2}Q_1V_1+\frac{1}{2}Q_2V_2$

sustituyendo la carga y el potencial al que se encuentra cada esfera (el de la interior ya la tenemos; el de la exterior se halla por superposición o por integración)

$U_e = \frac{1}{2}(2Q)\left(\frac{3Q}{8\pi\varepsilon_0 R}\right)+\frac{1}{2}(-Q)\left(\frac{Q}{4\pi\varepsilon_0R}\right) = \frac{5Q^2}{8\pi\varepsilon_0 R}$

También puede hallarse por integración de la densidad de energía

$U_e = \frac{1}{2}\int |\vec{E}|^2\,\mathrm{d}v$

Esta integral es más complicada, pero al depender solo del campo puede resolverse sin haber contestado las preguntas anteriores.

2 Dos cargas en el plano

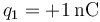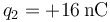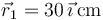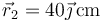Dos cargas puntuales $q_1=+1\,\mathrm{nC}$ y $q_2=+16\,\mathrm{nC}$ se encuentran respectivamente en $\vec{r}_1=30\,\vec{\imath}\,\mathrm{cm}$ y $\vec{r}_2=40\vec{\jmath}\,\mathrm{cm}$ . ¿En qué punto (en cm) se anula el campo eléctrico que producen?

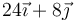
A $24\vec{\imath}+8\vec{\jmath}$
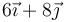
B $6\vec{\imath}+8\vec{\jmath}$
C $6\vec{\imath}+32\vec{\jmath}$
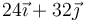
D $24\vec{\imath}+32\vec{\jmath}$

Solución

La respuesta correcta es la A.

La carga 1 es más pequeña que la 2. El punto donde el campo se anula se halla en la recta que pasa por las dos cargas y más cerca de la carga pequeña.

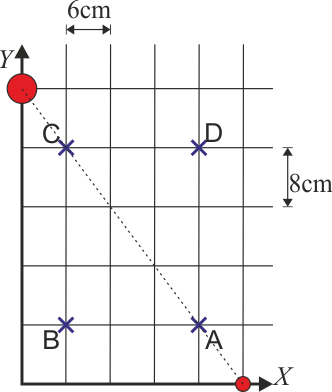
Situando los cuatro puntos propuestos en el plano es claro que la respuesta correcta es la A.

3 Separación de las placas de un condensador

Un condensador plano de capacidad $C 0$ tiene una de sus placas a tierra y la otra conectada a una fuente que mantiene fijado su potencial en $V 0$ . Se mueve una de las placas de forma que la distancia entre placas pasa a ser el triple de la inicial.

3.1 Pregunta 1

¿Cuánto varía la energía almacenada en el condensador?

A No cambia.
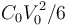
B Aumenta en $C_0V_0^2/6$
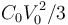
C Disminuye en $C_0V_0^2/3$
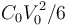
D Disminuye en $C_0V_0^2/6$

Solución

La respuesta correcta es la C.

Al separar las placas, la capacidad del condensador disminuye

$C = \frac{\varepsilon_0 S}{3a}=\frac{C_0}{3}$

Por tanto, la energía inicial vale

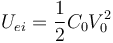
$U_{ei}=\frac{1}{2}C_0V_0^2$

y la final

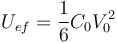
$U_{ef}=\frac{1}{6}C_0V_0^2$

siendo el incremento

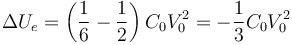
$\Delta U_e = \left(\frac{1}{6}-\frac{1}{2}\right)C_0V_0^2=-\frac{1}{3}C_0V_0^2$

3.2 Pregunta 3

¿Qué trabajo realiza el generador en este proceso?

A $+C_0V_0^2/6$
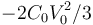
B $+2C_0 V_0^2/3$
C $-2C_0 V_0^2/3$
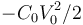
D $-C_0V_0^2/2$

Solución

La respuesta correcta es la C.

El trabajo realizado por el generador es

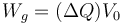
$W_g = (\Delta Q)V_0\,$

que en este caso vale

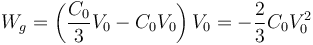
$W_g = \left(\frac{C_0}{3}V_0-C_0V_0\right)V_0=-\frac{2}{3}C_0V_0^2$

4 Afirmaciones sobre un conductor

¿Cuál de las siguientes afirmaciones es falsa en general para un conductor en equilibrio electrostático?

A Todo el conductor se encuentra al mismo potencial.
B No puede haber líneas de campo eléctrico que comiencen y acaben en el mismo conductor.
C El campo eléctrico justo en el exterior es perpendicular a la superficie del conductor.
D La carga total del conductor es nula.

Solución

La respuesta correcta es la D.

5 Dos cargas en una varilla

En los extremos de una varilla rígida se sitúan dos cargas $+ Q$ . La varilla se sitúa en el interior de un campo eléctrico uniforme que forma un cierto ángulo con la dirección de la varilla. ¿Qué efecto produce el campo eléctrico sobre el sistema?

A Una fuerza que tiende a desplazarla en la dirección del campo eléctrico, pero en sentido opuesto a éste.
B Un par que tiende a situarla perpendicularmente al campo eléctrico.
C Una fuerza que tiende a desplazarla en la dirección y sentido del campo eléctrico.
D Un par que tiende a alinearla con el campo eléctrico.

Solución

La respuesta correcta es la C.

Puesto que las dos cargas son del mismo signo, la fuerza eléctrica sobre ellas va en el mismo sentido. Por tanto no forman un par de fuerzas.

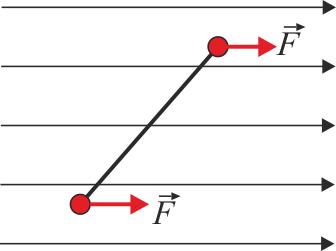
La resultante es una fuerza en la misma dirección del campo eléctrico y, por ser positivas las cargas, también en el mismo sentido.

6 Vuelco de un cilindro

Un cilindro vertical de paredes diatermas de 16²cm² de sección contiene de aire seco (gas ideal con $γ = 1.4$ ) estando cerrado herméticamente en su parte superior por un pistón de 4 kg de masa situado a 15 cm del fondo. En todo momento la presión exterior es de 100 kPa y la temperatura de 300 K.

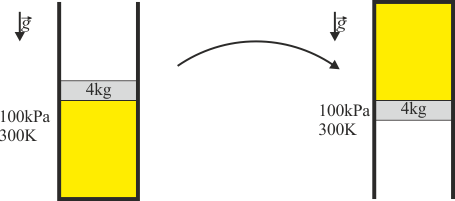
Se gira muy lentamente el cilindro hasta que el pistón queda en su parte inferior. Suponiendo $g\simeq 10\,\mathrm{m}/\mathrm{s}^2$ …

6.1 Pregunta 1

¿Cuál es la nueva distancia del pistón al fondo del cilindro?

A 20 cm
B 9 cm
C 25 cm
D Infinito, pues el pistón acaba cayendo por la boca del tubo.

Solución

La respuesta correcta es la C.

En el estado inicial el equilibrio mecánico se alcanza cuando la presión interior es capaz de compensar la acción combinada de la presión exterior y la debida al peso del pistón

$p_A = p_\mathrm{ext}+\frac{mg}{S}= 100\,\mathrm{kPa} + \frac{4\times 10}{16\times 10^{-4}}\,\mathrm{Pa}=125\,\mathrm{kPa}$

En el estado final, en cambio, es la presión exterior la que debe equilibrar a la interior y al peso

$p_B + \frac{mg}{S}=p_\mathrm{ext}\qquad\Rightarrow\qquad p_B = p_\mathrm{ext}-\frac{mg}{S}=75\,\mathrm{kPa}$

Al ser las paredes diatermas el proceso es a temperatura constante, por lo que la ley de los gases ideales se reduce a la ley de Boyle siendo el volumen $V = S h$

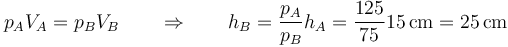
$p_A V_A = p_B V_B\qquad \Rightarrow\qquad h_B = \frac{p_A}{p_B}h_A=\frac{125}{75}15\,\mathrm{cm}=25\,\mathrm{cm}$

6.2 Pregunta 2

¿Cuánto calor entra en el aire de la cámara en este proceso?

A 0.0 J
B 12.3 J
C −12.3 J
D 15.3 J

Solución

La respuesta correcta es la D.

Puesto que el proceso es isotermo y cuasiestático el calor que entra en el sistema es

$Q=p_AV_A \ln\left(\frac{V_B}{V_A}\right)$

lo que da

$Q= 125\,\mathrm{kPa}\times (16\times 15)\mathrm{cm}^3\ln\left(\frac{25}{15}\right)= 15.3\,\mathrm{J}$

Test del Examen Parcial 2014-2015

De Laplace

Contenido

1 Campo con simetría esférica

1.1 Pregunta 1

1.2 Pregunta 2

1.3 Pregunta 3

2 Dos cargas en el plano

3 Separación de las placas de un condensador

3.1 Pregunta 1

3.2 Pregunta 3

4 Afirmaciones sobre un conductor

5 Dos cargas en una varilla

6 Vuelco de un cilindro

6.1 Pregunta 1

6.2 Pregunta 2

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES