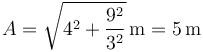Test de la prueba de control 2015-2016 (GIE)

De Laplace

Contenido

1 Velocidad variable
2 Incertidumbre relativa
3 Triedro de Frenet
- 3.1 Pregunta 1
- 3.2 Pregunta 2
4 Cálculo de unidades
5 Velocidad media
6 Caso de m.a.s.
- 6.1 Pregunta 1
- 6.2 Pregunta 2

1 Velocidad variable

Una partícula describe un movimiento rectilíneo en el que parte del reposo con velocidad inicial $v 0$ y su aceleración varía con el tiempo como

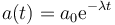
$a(t)=a_0\mathrm{e}^{-\lambda t}\,$

con $a 0$ y $λ$ constantes positivas.

¿Cómo cambia la velocidad de esta partícula con el tiempo?

A aumenta indefinidamente hasta infinito.
B disminuye indefinidamente hasta $-\infty$ .
C aumenta continuamente, tendiendo a un valor constante.
D disminuye gradualmente hasta cero.

Solución

La respuesta correcta es la C.

La aceleración, derivada de la velocidad, es siempre positiva. Por tanto la velocidad es una función creciente.

Por otro lado, al ser la aceleración una función que decae exponencialmente, su integral es finita, por lo que la velocidad no crece sin límite, sino que tiende a un valor constante

$v(t) = v_0+\int_0^t a_0\mathrm{e}^{-\lambda t}\mathrm{d}t=v_0+\frac{a_0}{\lambda}\left(1-\mathrm{e}^{-\lambda t}\right)\to v_0+\frac{a_0}{\lambda}$

2 Incertidumbre relativa

De un bloque de un material homogéneo se conoce su masa con una gran precisión, pero su volumen se conoce con una incertidumbre relativa del 1%. Si calculamos la densidad del material como $M / V$ la incertidumbre relativa de ésta es aproximadamente…

A -1%
B No tenemos información suficiente para saberla
C 2%
D 1%

Solución

La respuesta correcta es la D.

Si la incertidumbre relativa del volumen es del 1% quiere decir que su valor real puede hallarse en el intervalo

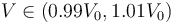
$V\in \left(0.99V_0,1.01V_0\right)$

siendo $V 0$ el valor medido para el volumen. Por tanto la densidad estará en el intervalo

$\rho_\mathrm{min}=\frac{M}{1.01V_0}=0.99\frac{M}{V_0}=0.99\rho_0\qquad\qquad \rho_\mathrm{max}=\frac{M}{0.99V_0}=1.01\frac{M}{V_0}=1.01\rho_0$

Por tanto su incertidumbre relativa es también del 1%.

3 Triedro de Frenet

En el movimiento de una partícula, en un instante dado el vector tangente a la trayectoria es $\vec{T}=0.64\vec{\imath}-0.60\vec{\jmath}+0.48\vec{k}$

3.1 Pregunta 1

¿Cuál de los siguientes vectores puede ser el vector normal, $\vec{N}$ , de dicho movimiento?

A $\vec{N}=-0.30\vec{\imath}+0.40\vec{k}$
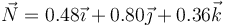
B $\vec{N}=0.48\vec{\imath}+0.80\vec{\jmath}+0.36\vec{k}$
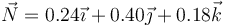
C $\vec{N}=0.24\vec{\imath}+0.40\vec{\jmath}+0.18\vec{k}$
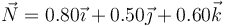
D $\vec{N}=0.80\vec{\imath}+0.50\vec{\jmath}+0.60\vec{k}$

Solución

La respuesta correcta es la B.

El vector normal debe ser unitario y ortogonal a $\vec{T}$ . El único unitario es el de la opción B.

3.2 Pregunta 2

Y dados los vectores $\vec{T}$ y $\vec{N}$ anteriores, ¿cuál puede ser el vector binormal, $\vec{B}$ ?

A $\vec{B}=-0.80\vec{\imath}+0.60\vec{k}$
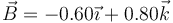
B $\vec{B}=-0.60\vec{\imath}+0.80\vec{k}$
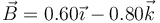
C $\vec{B}=0.60\vec{\imath}-0.80\vec{k}$
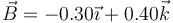
D $\vec{B}=-0.30\vec{\imath}+0.40\vec{k}$

Solución

La respuesta correcta es la B.

Se calcula como

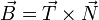
$\vec{B}=\vec{T}\times\vec{N}$

4 Cálculo de unidades

En un movimiento rectilíneo, la velocidad de una partícula depende de la posición como

$v=A(x^2+B)\,$

¿En qué se mide la constante A en el SI?

A 1/(m·s)
B 1/s
C m/s
D m³/s

Solución

La respuesta correcta es la A.

Por el principio de homogeneidad

$1\,\frac{\mathrm{m}}{\mathrm{s}}=[A](\mathrm{m})^2\qquad\Rightarrow\qquad [A]=\frac{1}{\mathrm{m}\cdot\mathrm{s}}$

5 Velocidad media

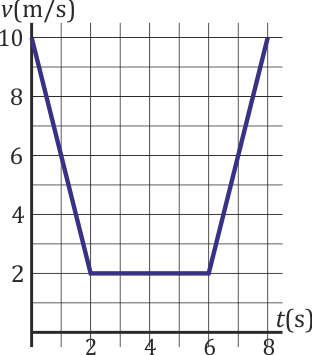
En un movimiento rectilíneo, la velocidad de una partícula como función del tiempo sigue la gráfica de la figura. ¿Cuánto vale la velocidad media en este intervalo de tiempo?

A 6 m/s
B 5 m/s
C 4 m/s
D 10 m/s

Solución

La respuesta correcta es la C.

Hallamos el desplazamiento como el área bajo la curva, que es la suma de tres trapecios (o de un rectángulo y dos triángulos)

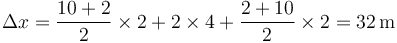
$\Delta x = \frac{10+2}{2}\times 2+2\times 4+\frac{2+10}{2}\times 2 = 32\,\mathrm{m}$

y queda la velocidad media

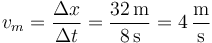
$v_m = \frac{\Delta x}{\Delta t}=\frac{32\,\mathrm{m}}{8\,\mathrm{s}}=4\,\frac{\mathrm{m}}{\mathrm{s}}$

6 Caso de m.a.s.

En un movimiento armónico simple de frecuencia 3 rad/s la amplitud compleja o fasor de la velocidad es 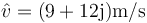$\hat{v}=(9+12\mathrm{j})\mathrm{m}/\mathrm{s}$ .

6.1 Pregunta 1

¿Cuanto vale la velocidad inicial de la partícula?

A 3 m/s
B 9 m/s
C 4 m/s
D 36 m/s

Solución

La respuesta correcta es la B.

El fasor de la elongación es el número complejo

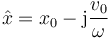
$\hat{x}=x_0-\mathrm{j}\frac{v_0}{\omega}$

y por tanto el de la velocidad

$\hat{v}=\mathrm{j}\omega\hat{x}=v_0+\mathrm{j}\omega x_0$

Igualando esta expresión a la del enunciado queda

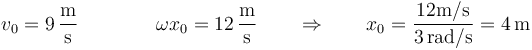
$v_0=9\,\frac{\mathrm{m}}{\mathrm{s}} \qquad\qquad \omega x_0=12\,\frac{\mathrm{m}}{\mathrm{s}}\qquad\Rightarrow\qquad x_0=\frac{12\mathrm{m}/\mathrm{s}}{3\,\mathrm{rad}/\mathrm{s}}=4\,\mathrm{m}$

por lo que la velocidad inicial es 9m/s.

6.2 Pregunta 2

Para este movimiento, ¿cuánto vale la amplitud de las oscilaciones?

A 5 m
B 15 m
C 3 m
D 4 m

Solución

La respuesta correcta es la A.

La amplitud de las oscilaciones en un m.a.s. se puede calcular a partir de las condiciones iniciales como

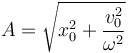
$A=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}$

que sustituyendo los valores de la pregunta anterior da

$A=\sqrt{4^2+\frac{9^2}{3^2}}\,\mathrm{m}=5\,\mathrm{m}$

Test de la prueba de control 2015-2016 (GIE)

De Laplace

Contenido

1 Velocidad variable

2 Incertidumbre relativa

3 Triedro de Frenet

3.1 Pregunta 1

3.2 Pregunta 2

4 Cálculo de unidades

5 Velocidad media

6 Caso de m.a.s.

6.1 Pregunta 1

6.2 Pregunta 2

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES