Test de la primera convocatoria de Física I 2015-2016 (GIE) (2ª parte)

De Laplace

Contenido

1 Movimiento circular
2 Vértices de un tetraedro
- 2.1 Pregunta 1
- 2.2 Pregunta 2
3 Velocidad media
4 Caso de m.a.s.
- 4.1 Pregunta 1
- 4.2 Pregunta 2
5 Anilla ensartada
- 5.1 Pregunta 1
- 5.2 Pregunta 2

1 Movimiento circular

En todo movimiento circular es constante\ldots

A el vector normal.
B el vector binormal.
C la rapidez.
D el vector tangente.

Solución

La respuesta correcta es la B.

Un movimiento circular es un movimiento plano, en el que la velocidad y la aceleración están contenidas siemrpe en el mismo plano. El vector binormal, que es el unitario ortogonal a este plano, permanece entonces constante.

2 Vértices de un tetraedro

Sean $\vec{A}$ , $\vec{B}$ y $\vec{C}$ tres vectores unitarios tales que $\vec{A}$ apunta en la dirección del eje OX, $\vec{B}$ está en el plano OXY formando un ángulo $π / 3$ con $\vec{A}$ , mientras que $\vec{C}$ forma el mismo ángulo $π / 3$ con $\vec{A}$ y con $\vec{B}$ .

2.1 Pregunta 1

¿Cuál de los siguientes es el vector $\vec{B}$ ?

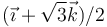
A $(\vec{\imath}+\sqrt{3}\vec{k})/2$
B $(\vec{\imath}+\sqrt{3}\vec{\jmath})/2$
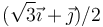
C $(\sqrt{3}\vec{\imath}+\vec{\jmath})/2$
D $(\sqrt{3}\vec{\imath}-\vec{k})/2$

Solución

La respuesta correcta es la B.

El vector $\vec{B}$ está en el plano OXY, por tanto no puede tener componente en la dirección del vector $\vec{k}$ . Esto descarta las opciones A y D.

Como forma un ángulo de π/3 con $\vec{A}$ debe cumplirse

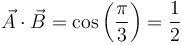
$\vec{A}\cdot\vec{B}=\cos\left(\frac{\pi}{3}\right)=\frac{1}{2}$

Como $\vec{A}=\vec{\imath}$ esta condición solo se cumple para el vector de la opción B

$\vec{A}\cdot\vec{B}=1\cdot\frac{1}{2}+0+0 = \frac{1}{2}$

2.2 Pregunta 2

¿Y el vector $\vec{C}$ ?

A $(1/2)\vec{\imath}-(\sqrt{3}/6)\vec{\jmath}+(\sqrt{6}/3)\vec{k}$
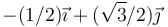
B $(1/2)\vec{\imath}-(\sqrt{3}/2)\vec{\jmath}$
C $-(1/2)\vec{\imath}+(\sqrt{3}/2)\vec{\jmath}$
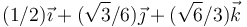
D $(1/2)\vec{\imath}+(\sqrt{3}/6)\vec{\jmath}+(\sqrt{6}/3)\vec{k}$

Solución

La respuesta correcta es la D.

El vector $\vec{C}$

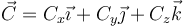
$\vec{C}=C_x\vec{\imath}+C_y\vec{\jmath}+C_z\vec{k}$

forma un ángulo de π/3 tanto con $\vec{A}$ como con $\vec{B}$ , por lo que debe cumplirse

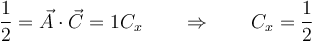
$\frac{1}{2}=\vec{A}\cdot\vec{C}=1·C_x \qquad\Rightarrow\qquad C_x = \frac{1}{2}$

lo que descarta la opción C. También debe cumplirse

$\frac{1}{2}=\vec{B}\cdot\vec{C}=\frac{1}{2}·C_x +\frac{\sqrt{3}}{2}C_y\qquad\Rightarrow\qquad C_y = \frac{1-C_x}{\sqrt{3}}=\frac{\sqrt{3}}{6}$

por lo que la opción es la D.

3 Velocidad media

Una partícula se mueve sobre una recta con una velocidad dependiente de la posición como indica la figura.

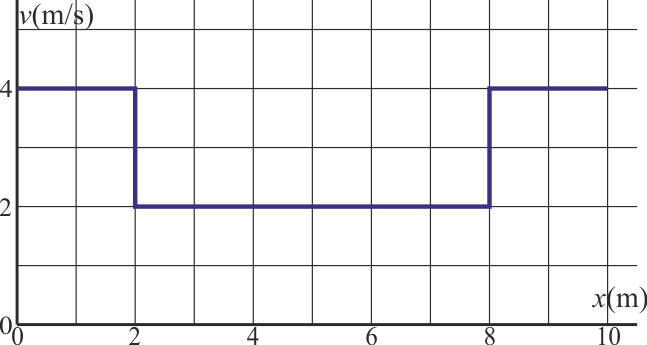
¿Cuál es la velocidad media en el tramo 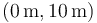$(0\,\mathrm{m},10\,\mathrm{m})$ ?

A 3.0 m/s
B 2.0 m/s
C 2.8 m/s
D 2.5 m/s

Solución

La respuesta correcta es la D.

La velocidad media es el cociente entre el desplzamiento y el intervalo de tiempo empleado en recorrerlo. En este caso conocemos el desplazamiento (10 m); nos queda conocer el intervalo.

El movimiento se compone de tres tramos. El tiempo empleado en recorrer cada uno es

$\Delta t_1 = \frac{2\,\mathrm{m}}{4\,\mathrm{m}/\mathrm{s}} = 0.5\,\mathrm{s}\qquad\qquad \Delta t_2 = \frac{6\,\mathrm{m}}{2\,\mathrm{m}/\mathrm{s}} = 3.0\,\mathrm{s}\qquad\qquad \Delta t_3 = \Delta t_1 = 0.5\,\mathrm{s}$

siendo el intervalo total

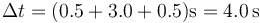
$\Delta t = (0.5+3.0+0.5)\mathrm{s} = 4.0\,\mathrm{s}$

y la velocidad media

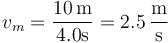
$v_m=\frac{10\,\mathrm{m}}{4.0\mathrm{s}}=2.5\,\frac{\mathrm{m}}{\mathrm{s}}$

4 Caso de m.a.s.

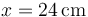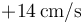Un oscilador armónico tiene frecuencia $\omega=2\,\mathrm{rad}/\mathrm{s}$ . Su elongación inicial es $x=24\,\mathrm{cm}$ y su velocidad inicial es $+14\,\mathrm{cm}/\mathrm{s}$ .

4.1 Pregunta 1

¿Cuánto vale su velocidad máxima en cm/s?

A 12.5
B 100.0
C 25.0
D 50.0

Solución

La respuesta correcta es la D.

La amplitud de las oscilaciones se puede calcular a partir de las condiciones iniciales

$A=\sqrt{x_0^2+\left(\frac{v_0}{\omega}\right)^2}=\sqrt{24^2+7^2}\,\mathrm{cm}=25\,\mathrm{cm}$

La velocidad en un m.a.s. es también una sinusoide de amplitud

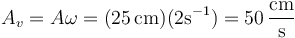
$A_v = A\omega = (25\,\mathrm{cm})(2\mathrm{s}^{-1})=50\,\frac{\mathrm{cm}}{\mathrm{s}}$

Alternativamente, podemos hallar en primer lugar el fasor de la elongación

$\hat{x}=x_0+\mathrm{j}\frac{v_0}{\omega}=(24+7\mathrm{j})\mathrm{cm}$

A partir de este el de la velocidad

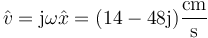
$\hat{v}=\mathrm{j}\omega \hat{x}=(14-48\mathrm{j})\frac{\mathrm{cm}}{\mathrm{s}}$

y la velocidad máxima es el módulo de esta amplitud compleja

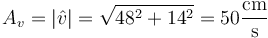
$A_v=|\hat{v}| = \sqrt{48^2+14^2}=50\frac{\mathrm{cm}}{\mathrm{s}}$

4.2 Pregunta 2

¿Cuánto tarda en pasar por primera vez por $x=31\,\mathrm{cm}$ ?

A 0.5 s
B 1.0 s
C 2.0 s
D No pasa nunca por ese punto.

Solución

La respuesta correcta es la D.

Según se ha visto en la pregunta anterior, la amplitud es de 25 cm. Puesto que la posición de equilibrio es x=0, nunca puede llegar a una elongación de 31 cm.

5 Anilla ensartada

Dos varillas de gran longitud están articuladas en el eje OX, estando a una distancia $b$ sus puntos de articulación. Una de las varillas gira con velocidad angular $Ω$ y la otra con velocidad angular $2Ω$ . Una anilla se encuentra ensartada en la intersección de ambas varillas, como indica la figura. Inicialmente las dos varillas están alineadas.

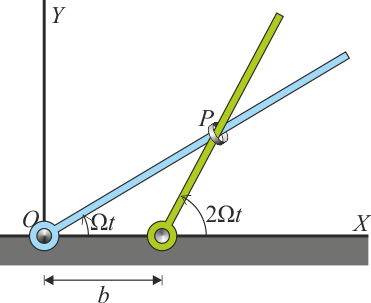
5.1 Pregunta 1

¿Qué trayectoria sigue la anilla?

A Parabólica.
B Hiperbólica.
C Circular.
D Rectilínea.

Solución

La respuesta correcta es la C.

Si P es la posición de la partícula y A es la de la articulación de la barra de la derecha, la distancia AP es constante

$\left|\overrightarrow{AP}\right| =b=\mathrm{cte}$

Esto se explica porque el triángulo OAP es isósceles.

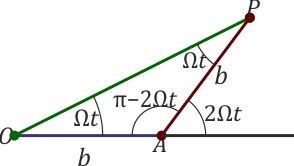
El ángulo en O vale $α O = Ω t$ , el ángulo en A es el suplementario de $2Ω t$

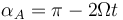
$\alpha_A=\pi-2\Omega t\,$

y por tanto el ángulo en P mide

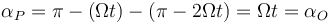
$\alpha_P = \pi-(\Omega t)-(\pi-2\Omega t)= \Omega t=\alpha_O\,$

Como los dos ángulos en O y en P son iguales, los lados correspondientes también lo son.

Si la distancia AP es constante, la partícula describe un movimiento circular centrado en A.

También se puede determinar de un modo más “mecánico” separando en componentes cartesianas. Si $r 1$ y $r 2$ son las distancias a las articulaciones o y A tenemos

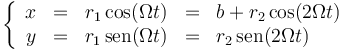
$\left\{\begin{array}{rcccl} x & = & r_1\cos(\Omega t) & = & b + r_2\cos(2\Omega t) \\ y & = & r_1\,\mathrm{sen}(\Omega t) & = & r_2\,\mathrm{sen}(2\Omega t) \end{array}\right.$

De la segunda, desarrollando el seno del ángulo doble queda

$r_1\,\mathrm{sen}(\Omega t) = 2r_2\,\mathrm{sen}(\Omega t)\cos(\Omega t)\qquad\Rightarrow\qquad r_1 = 2\cos(\Omega t)$

si ahora sustituimos en la primara y desarrollamos el coseno del ángulo doble

$2r_2\cos^2(\Omega t) = b + r_2(\cos^2(\Omega t) - \mathrm{sen}^2(\Omega t)) \qquad\Rightarrow\qquad r_2(\cos^2(\Omega t) + \mathrm{sen}^2(\Omega t)) = r_2 = b$

5.2 Pregunta 2

En los ejes de la figura, ¿cuánto vale su aceleración tangencial cuando $Ω t = π / 4$ ?

A $\Omega^2b(-\vec{\imath}+\vec{\jmath})$
B $\vec{0}$
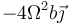
C $-4\Omega^2b\vec{\jmath}$
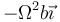
D $-\Omega^2b\vec{\imath}$

Solución

La respuesta correcta es la B.

La partícula describe un movimiento circular centrado en A, y además el ángulo con el eje X aumenta a ritmo constante.

Por tanto, el movimiento es uniforme y la aceleración tangencial es nula.

Test de la primera convocatoria de Física I 2015-2016 (GIE) (2ª parte)

De Laplace

Contenido

1 Movimiento circular

2 Vértices de un tetraedro

2.1 Pregunta 1

2.2 Pregunta 2

3 Velocidad media

4 Caso de m.a.s.

4.1 Pregunta 1

4.2 Pregunta 2

5 Anilla ensartada

5.1 Pregunta 1

5.2 Pregunta 2

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES