Test de la primera convocatoria de Física I 2013-2014 (GIE) (1ª parte)
De Laplace
Contenido |
1 Sólido en forma de T
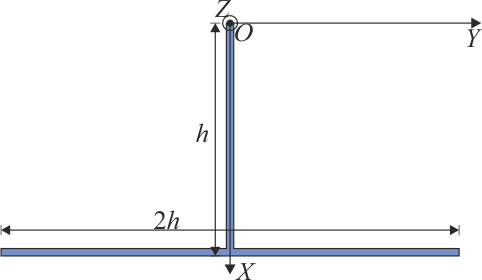
Se tiene un sólido en forma de T formado por dos varillas homogéneas de la misma densidad, siendo el travesaño de longitud 2h y el mástil de longitud h. La masa total del sólido es M
1.1 Pregunta 1
En el sistema de ejes de la figura, ¿dónde se encuentra el centro de masas del sistema?
- A

- B
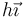
- C
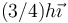
- D
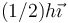
- A
- Solución
La respuesta correcta es la A.
La pieza está formada por dos partes. Cada una es una barra, una con masa el doble que la otra, y cada una con su centro de masa en su centro geométrico.
Para el mástil, se cumple

y para el travesaño

El centro de masas del sólido completo será

1.2 Pregunta 2
¿Cuánto vale su momento de inercia respecto a un eje perpendicular al plano de la T y que pasa por el extremo O del mástil?
- A (1 / 3)Mh2.
- B (2 / 3)Mh2.
- C Mh2.
- D 3Mh2.
- Solución
La respuesta correcta es la C.
El momento de inercia es suma del del mástil más el del travesaño. En ambos casos aplicamos que el momento de inercia de una varilla respecto a un eje que pasa por su centro y es perpendicular a ella vale
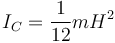
y respecto a un eje paralelo a éste podemos hallarlo aplicando el teorema de Steiner
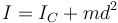
Para el mástil tenemos entonces
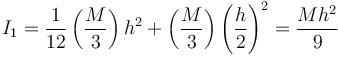
y para el travesaño
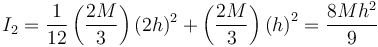
Sumando las dos partes

2 Cálculo de velocidad
Una partícula de masa 1 kg se mueve por el eje OX de forma que cuando pasa por x = 0 su velocidad es +2 m/s. Sobre la partícula actúa una fuerza en la dirección del mismo eje, 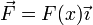 cuya gráfica es la de la figura.
cuya gráfica es la de la figura.

¿Cuál es la velocidad de la partícula cuando pasa por x = 10m?
- A +5 m/s.
- B Es imposible que llegue a ese punto.
- C +6 m/s.
- D +2 m/s.
- Solución
La respuesta correcta es la C.
El teorema de las fuerzas vivas establece que
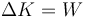
En este caso, empleando el SI para todas las variables
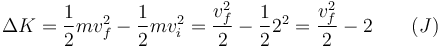
mientras que el trabajo es igual a la integral
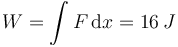
El valor de la integral corresponde al área bajo la curva, que en este caso es igual a la de un triángulo.
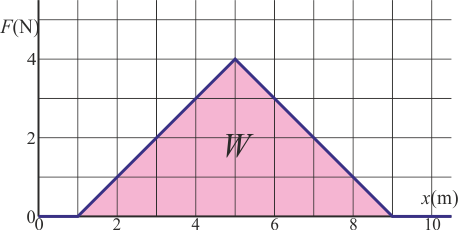
Este trabajo es positivo, como corresponde a que la fuerza vaya en el mismo sentido del movimiento y acelere la partícula.
Igualando las dos cantidades

3 Velocidades en un sólido
En el movimiento de un sólido, el punto O(0,0,0) tiene velocidad 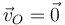 , el punto A(1,0,0) tiene velocidad
, el punto A(1,0,0) tiene velocidad  y el punto B(0,1,0) tiene velocidad
y el punto B(0,1,0) tiene velocidad  (todo en el SI). ¿Qué tipo de movimiento describe el sólido?
(todo en el SI). ¿Qué tipo de movimiento describe el sólido?
- A Rotación en torno al origen alrededor de un eje paralelo a
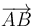 .
.
- B No hay información suficiente para saber cómo se mueve.
- C Rotación en torno al eje que pasa por A y B.
- D Estas velocidades no son posibles en un sólido.
- A Rotación en torno al origen alrededor de un eje paralelo a
- Solución
La respuesta correcta es la A.
Comprobamos en primer lugar que se cumple la condición de rigidez. Para O y A

Para O y B el cálculo es casi idéntico. Para A y B es obvio que se cumple pues las velocidades son iguales.
las velocidades no son todas iguales, luego no es una traslación. El punto O tiene velocidad nula, luego se trata de una rotación en torno a un eje que pasa por O. A y B tienen velocidades iguales. Por tanto el eje de rotación es paralelo a la recta que pasa por A y B.
4 Oscilador amortiguado
Una masa m está unida a un resorte de constante k. Para reducir sus oscilaciones se emplea un amortiguador que produce un rozamiento viscoso 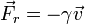 . Si la constante γ es igual a
. Si la constante γ es igual a  , este oscilador…
, este oscilador…
- A tiene amortiguamiento crítico.
- B no se puede saber de qué tipo es.
- C es subamortiguado.
- D es sobreamortiguado.
- Solución
La respuesta correcta es la C.
Para que un oscilador tenga amortiguamiento crítico debe cumplirse
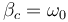
o, empleando las vriables del sistema

Como el valor que se da es menor que este, γ < γc, se trata de un oscilador subamortiguado.
5 Palanca
Para levantar un peso de 1 kN se emplea una palanca de 2 m de longitud. El peso se coloca en su extremo B. En el extremo A, opuesto al peso, se aplica una fuerza hacia abajo de 250 N. ¿A qué distancia de A, como mínimo, debe colocarse el fulcro para poder levantar el peso?
- A 180 cm.
- B 40 cm.
- C 160 cm.
- D 150 cm.
- Solución
La respuesta correcta es la C.
Si bA y bB son las distancias de A y B, respectivamente, al fulcro, se cumple

Por otro lado, la condición de posición mínima la da el caso en que haya equilibrio. Tomando momentos respecto al punto de apoyo O, debe cumplirse
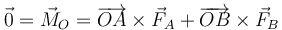
Cada momento es igual a la fuerza correspondiente multiplicada por el brazo correspondiente, lo que da
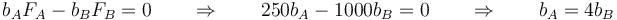
y puesto que la longitud total son 2 metros

6 Péndulo rotatorio
En la ilustración de la figura una masa m está sujeta a un péndulo, pero gira sin oscilar. ¿Cuánto vale la velocidad angular con la que gira el soporte?
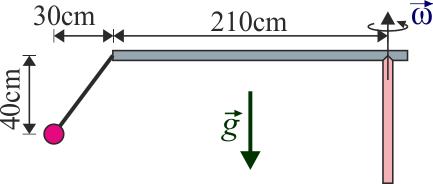
- A 4.20 rad/s
- B 1.75 rad/s.
- C 3.50 rad/s.
- D Depende del valor de la masa.
- Solución
La respuesta correcta es la B.
La masa describe un movimiento circular uniforme, por lo que su aceleración es puramente normal. Por tanto se cumple la segunda ley de Newton en la forma
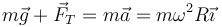
Tomando un sistema de ejes centrado en la masa en el que el eje OX es horizontal y hacia la derecha de la figura. El peso va en la dirección vertical
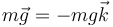
mientras que la tensión del hilo va a lo largo de éste
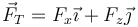
donde, por ser paralelo al hilo

La segunda ley de Newton, separada en componentes da

Dividiendo una ecuación por la otra
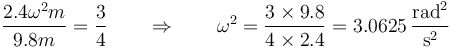
y tomando la raíz cuadrada
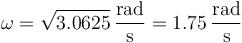
7 Constante de movimiento
En el movimiento de un oscilador armónico tridimensional (que cumple 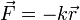 ), ¿cuál de las siguientes cantidades se conserva?
), ¿cuál de las siguientes cantidades se conserva?
- A La energía potencial
- B El momento cinético respecto al origen de coordenadas.
- C La cantidad de movimiento.
- D La energía cinética.
- Solución
La respuesta correcta es la B.
El movimiento de una partícula sometida a una fuerza central

como es el caso del oscilador armónico, conserva el momento cinético respecto al centro de fuerzas, al ser paralela la fuerza al vector de posición






