Test de la 2ª convocatoria 2017-2018 3ª parte (GIE)
De Laplace
Contenido |
1 Rotación de un sólido
Un sólido rígido describe un movimiento tal que en un instante dado su velocidad angular es 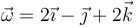 (rad/s) y la velocidad del punto A(2,1,2) (m) es
(rad/s) y la velocidad del punto A(2,1,2) (m) es 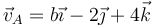 (m/s).
(m/s).
1.1 Pregunta 1
¿Cuánto debe valer la cantidad b si se sabe que el movimiento instantáneo es de rotación?
- A 4 m/s.
- B −5 m/s.
- C −3 m/s.
- D no hay suficiente información para saberlo.
- Solución
La respuesta correcta es la B.
La velocidad de cada punto debe ser ortogonal a la velocidad angular
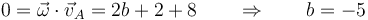
1.2 Pregunta 2
Para el movimiento anterior, ¿Cuál de los siguientes puntos pertenece al EIR?
- A B(2,-1,1)
- B C(1,3,-1)
- C O(0,0,0)
- D D(4,-2,-3)
- Solución
La respuesta correcta es la A.
En una rotación los puntos del eje cumplen
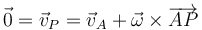
Probando con los distintos puntos, a la primera sale que 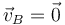 .
.
2 Rodadura de un cilindro
Un rodillo cilíndrico macizo y homogéneo rueda sin deslizar por una superficie horizontal. ¿Qué fracción de su energía cinética total es energía cinética de traslación?
- A 33%.
- B 67%.
- C 50%.
- D Depende del radio y la masa del cilindro.
- Solución
La respuesta correcta es la B.
La energía cinética de un sólido es

En el caso de un rodillo macizo rodante

y por tanto
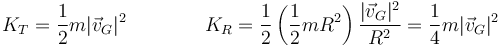
Siendo la proporción
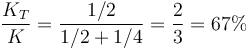
3 Par prismático
Dos sólidos se hallan engarzados por un par prismático. ¿Cuántos grados de libertad tiene el movimiento relativo entre los dos sólidos?
- A 1.
- B 2.
- C 3.
- D 6.
- Solución
La respuesta correcta es la A.
4 Sistema de fuerzas
Sobre un sólido actúan simultáneamente tres fuerzas: 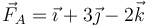 aplicada en A(2,1,0),
aplicada en A(2,1,0), 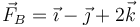 aplicada en B(1,0,0) y
aplicada en B(1,0,0) y 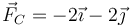 aplicada en C(0,-2,1) (fuerzas en N, posiciones en m). ¿A qué se reduce este sistema de fuerzas?
aplicada en C(0,-2,1) (fuerzas en N, posiciones en m). ¿A qué se reduce este sistema de fuerzas?
- A Es un sistema nulo.
- B Un par de fuerzas.
- C Una fuerza única.
- D Un tornillo.
- Solución
La respuesta correcta es la A.
No hay más que calcular la resultante
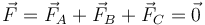
y el momento resultante
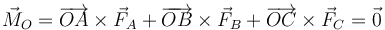
5 Barra que cuelga
Una barra rígida ideal, sin masa, de 60 cm tiene en uno de sus extremos una pesa de 30 N y en el otro una de 10 N. La barra está suspendida del techa por otras dos varillas verticales, engarzadas en puntos O y A de la barra, situados cada uno a 20 cm del extremo. Empleando el sistema de ejes de la figura, ¿cuánto vale la fuerza que ejerce cada una de las varillas de las que cuelga el sistema?

- A
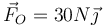 ;
; 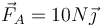 .
.
- B
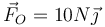 ;
; 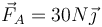 .
.
- C
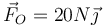 ;
; 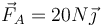 .
.
- D
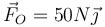 ;
; 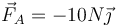 .
.
- A
- Solución
La respuesta correcta es la D.





