Test de la 1ª convocatoria Física II 2016-2017 2ª parte (GIE)

De Laplace

Contenido

1 Energía de cuatro cargas
2 Anillo cargado
- 2.1 Pregunta 1
- 2.2 Pregunta 2
3 Campo de hilos
4 Tres placas conductoras
- 4.1 Pregunta 1
- 4.2 Pregunta 2

1 Energía de cuatro cargas

Se tienen 4 cargas puntuales, dos de ellas de valor +q y otras dos de valor -q situadas en los vértices de un tetraedro regular. En este sistema la energía electrostática almacenada…

A es siempre positiva.
B es siempre negativa.
C es siempre nula.
D puede ser positiva o negativa, dependiendo de en qué vértice se sitúa cada carga.

Solución

La respuesta correcta es la B.

2 Anillo cargado

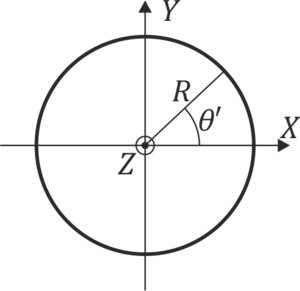
Un anillo de radio R se encuentra cargado con una densidad lineal de carga

λ = λ 0 cos 2 (θ')

. El anillo se encuentra situado en el plano OXY, centrado en el origen.

θ'

es la coordenada angular en cilíndricas (ángulo que el vector de posición forma con OX).

2.1 Pregunta 1

¿Cuánto vale la carga total del anillo?

A $2π R λ 0 cos 2 (θ')$ .
B $πλ 0 R$ .
C 0.
D $λ 0 R / 2$ .

Solución

La respuesta correcta es la B.

2.2 Pregunta 2

¿Cuánto vale el campo eléctrico en el centro del anillo?

A $\vec{0}$
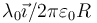
B $\lambda_0 \vec{\imath}/2\pi{}\varepsilon_0 R$
C $\lambda_0 \vec{\jmath}/2\pi{}\varepsilon_0 R$
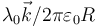
D $\lambda_0 \vec{k}/2\pi{}\varepsilon_0 R$

Solución

La respuesta correcta es la A.

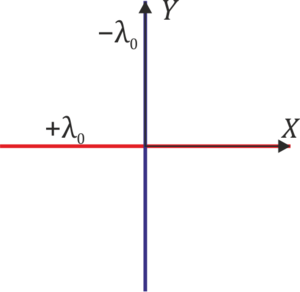
3 Campo de hilos

Una línea rectilínea infinita se halla cargada con una densidad

+ λ 0

y situada sobre el eje OX. Una segunda línea se halla sobre el eje OY y almacena una densidad de carga

- λ 0

. ¿Cuánto vale el campo eléctrico en los puntos del plano OXY?

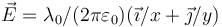
A $\vec{E}=\lambda_0/(2\pi{}\varepsilon_0 ) (\vec{\imath}/x+\vec{\jmath}/y)$
B $\vec{E}=\lambda_0/(2\pi{}\varepsilon_0 ) (\vec{\imath}/x-\vec{\jmath}/y)$
C $\vec{E}=\lambda_0/(2\pi{}\varepsilon_0 ) (-\vec{\imath}/x+\vec{\jmath}/y)$
D $\vec{E}=\lambda_0/(2\pi{}\varepsilon_0 ) ((x\vec{\imath}+y\vec{\jmath})/(x^2+y^2 ))$

Solución

La respuesta correcta es la B.

4 Tres placas conductoras

Se tiene un sistema de 3 placas conductoras cuadradas de lado b situadas paralelamente como se indica en la figura. la distancia entre dos placas consecutivas es a. El sistema está sumergido hasta la mitad en un líquido dieléctrico de permitividad absoluta $\varepsilon$ y el resto está vacío.

4.1 Pregunta 1

Inicialmente las placas están situadas horizontalmente. ¿Cuánto vale la carga en la placa central?

A 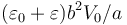$(\varepsilon_0+\varepsilon) b^2 V_0 /a$ .
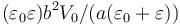B $(\varepsilon_0 \varepsilon) b^2 V_0/(a(\varepsilon_0+\varepsilon))$ .
C $(\varepsilon_0+\varepsilon) b^2 V_0 /(2a)$ .
D $0$ .

Solución

La respuesta correcta es la A.

4.2 Pregunta 2

Se gira el sistema 90° de manera que cada espacio entre placas se llena hasta la mitad de dieléctrico. ¿Cuánto vale ahora la carga de la placa central?

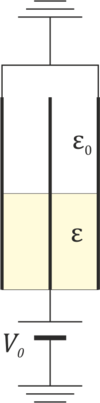
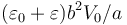
A $(\varepsilon_0+\varepsilon) b^2 V_0 /a$
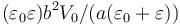B $(\varepsilon_0 \varepsilon) b^2 V_0 /(a(\varepsilon_0+\varepsilon))$ .
C $(\varepsilon_0+\varepsilon) b^2 V_0 /(2a)$ .
D $0$ .

Solución

La respuesta correcta es la A.

Test de la 1ª convocatoria Física II 2016-2017 2ª parte (GIE)

De Laplace

Contenido

1 Energía de cuatro cargas

2 Anillo cargado

2.1 Pregunta 1

2.2 Pregunta 2

3 Campo de hilos

4 Tres placas conductoras

4.1 Pregunta 1

4.2 Pregunta 2

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES