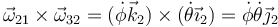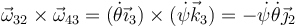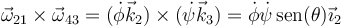Suspensión de tres ejes (CMR)

De Laplace

Contenido

1 Enunciado
2 Relaciones entre bases
3 Velocidad angular
4 Aceleración angular

1 Enunciado

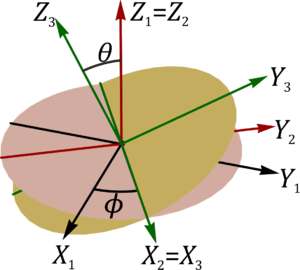
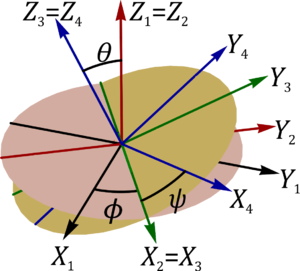
El sistema de los ángulos de Euler para describir cualquier rotación puede modelarse con una suspensión cardán de tres ejes, similar al del problema anterior pero con un cuarto sólido interior. El sólido 4 forma un ángulo ψ con el 3, siendo su eje de giro $O Z 3 = O Z 4$

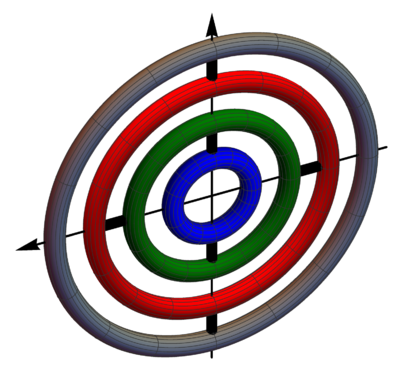
Indique las relaciones entre las bases ligadas a cada sólido
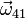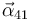Exprese la velocidad angular $\vec{\omega}_{41}$ y la aceleración angular $\vec{\alpha}_{41}$ .

2 Relaciones entre bases

Este problema es una continuación del de la suspensión Cardán de dos ejes, por lo que haremos uso de los resultados que allí se obtienen.

Tal como se ve en dicho porblema, la relación entre el sistema 1 y el 2 es

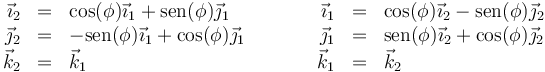
$\begin{array}{rclcrcl} \vec{\imath}_2&=&\cos(\phi)\vec{\imath}_1+\mathrm{sen}(\phi)\vec{\jmath}_1&\qquad&\vec{\imath}_1&=&\cos(\phi)\vec{\imath}_2-\mathrm{sen}(\phi)\vec{\jmath}_2\\ \vec{\jmath}_2&=&-\mathrm{sen}(\phi)\vec{\imath}_1+\cos(\phi)\vec{\jmath}_1&\qquad&\vec{\jmath}_1&=&\mathrm{sen}(\phi)\vec{\imath}_2+\cos(\phi)\vec{\jmath}_2\\ \vec{k}_2&=&\vec{k}_1&\qquad&\vec{k}_1&=&\vec{k}_2 \end{array}$

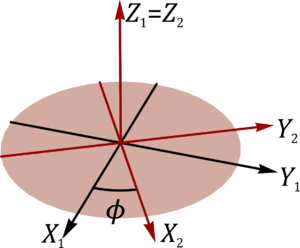
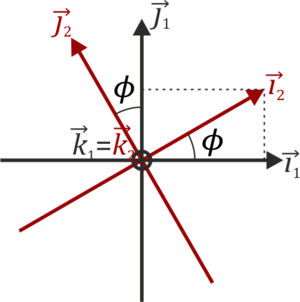
y entre el 2 y el 3

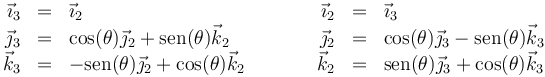
$\begin{array}{rclcrcl} \vec{\imath}_3&=&\vec{\imath}_2&\qquad&\vec{\imath}_2&=&\vec{\imath}_3\\ \vec{\jmath}_3&=&\cos(\theta)\vec{\jmath}_2+\mathrm{sen}(\theta)\vec{k}_2&\qquad&\vec{\jmath}_2&=&\cos(\theta)\vec{\jmath}_3-\mathrm{sen}(\theta)\vec{k}_3\\ \vec{k}_3&=&-\mathrm{sen}(\theta)\vec{\jmath}_2+\cos(\theta)\vec{k}_2&\qquad&\vec{k}_2&=&\mathrm{sen}(\theta)\vec{\jmath}_3+\cos(\theta)\vec{k}_3 \end{array}$

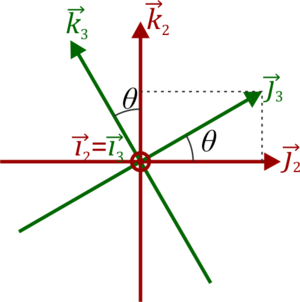
La relación entre es el sistema 3 y el 4 es de nuevo una rotación en torno a un eje OZ por lo que las relaciones son análogas a las primeras

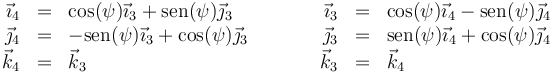
$\begin{array}{rclcrcl} \vec{\imath}_4&=&\cos(\psi)\vec{\imath}_3+\mathrm{sen}(\psi)\vec{\jmath}_3&\qquad&\vec{\imath}_3&=&\cos(\psi)\vec{\imath}_4-\mathrm{sen}(\psi)\vec{\jmath}_4\\ \vec{\jmath}_4&=&-\mathrm{sen}(\psi)\vec{\imath}_3+\cos(\psi)\vec{\jmath}_3&\qquad&\vec{\jmath}_3&=&\mathrm{sen}(\psi)\vec{\imath}_4+\cos(\psi)\vec{\jmath}_4\\ \vec{k}_4&=&\vec{k}_3&\qquad&\vec{k}_3&=&\vec{k}_4 \end{array}$

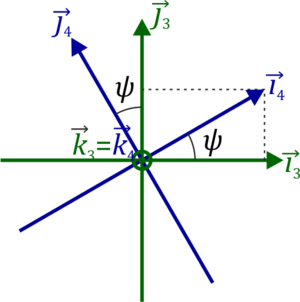
Por sustituciones sucesivas podemos obtener las relaciones entre dos bases cualesquiera de las 4 implicadas.

3 Velocidad angular

La velocidad angular {41} es la composición de las tres velocidades angulares individuales

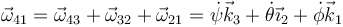
$\vec{\omega}_{41}=\vec{\omega}_{43}+\vec{\omega}_{32}+\vec{\omega}_{21}=\dot{\psi}\vec{k}_3+\dot{\theta}\vec{\imath}_2+\dot{\phi}\vec{k}_1$

En este caso, la expresión más sencilla se obtiene mezclando diferentes bases. Si deseamos expresar esta velocidad angular empleando una sola base debemos hacer uso de las relaciones anteriores. Así, para el sistema 3

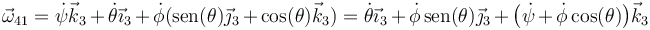
$\vec{\omega}_{41}=\dot{\psi}\vec{k}_3+\dot{\theta}\vec{\imath}_3+\dot{\phi}(\mathrm{sen}(\theta)\vec{\jmath}_3+\cos(\theta)\vec{k}_3)=\dot{\theta}\vec{\imath}_3+\dot{\phi}\,\mathrm{sen}(\theta)\vec{\jmath}_3+\big(\dot{\psi}+\dot{\phi}\cos(\theta)\big)\vec{k}_3$

Si deseamos la expresión en el sistema fijo 1 o en el ligado 4, hay que sustituir de nuevo, resultando expresiones más complicadas.

4 Aceleración angular

De manera similar se calcula la aceleración angular. Aplicamos la fórmula de composición correspondiente

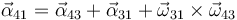
$\vec{\alpha}_{41}=\vec{\alpha}_{43}+\vec{\alpha}_{31}+\vec{\omega}_{31}\times\vec{\omega}_{43}$

y descomponiendo a su vez el movimiento {31}

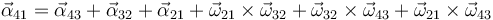
$\vec{\alpha}_{41}=\vec{\alpha}_{43}+\vec{\alpha}_{32}+\vec{\alpha}_{21}+\vec{\omega}_{21}\times\vec{\omega}_{32}+\vec{\omega}_{32}\times\vec{\omega}_{43}+\vec{\omega}_{21}\times\vec{\omega}_{43}$

Sustituimos aquí las expresiones individuales y queda

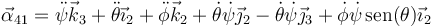
$\vec{\alpha}_{41}=\ddot{\psi}\vec{k}_3+\ddot{\theta}\vec{\imath}_2+\ddot{\phi}\vec{k}_2+\dot{\theta}\dot{\psi}\vec{\jmath}_2-\dot{\theta}\dot{\psi}\vec{\jmath}_3+\dot{\phi}\dot{\psi}\,\mathrm{sen}(\theta)\vec{\imath}_2$

donde hemos aplicado que