Suspensión cardán de dos ejes (CMR)

De Laplace

Contenido

1 Enunciado
2 Relaciones entre bases
- 2.1 Entre la base 1 y la 2
- 2.2 Entre la base 2 y la 3
3 Velocidades angulares
4 Aceleraciones angulares

1 Enunciado

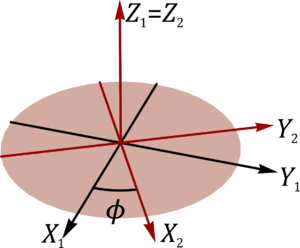
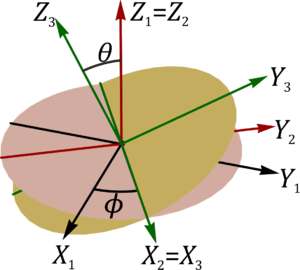
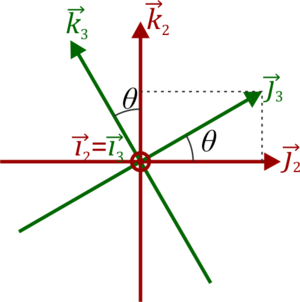
Una suspensión Cardán de dos ejes puede modelarse mediante tres aros concéntricos (gimbal) articulados sobre ejes perpendiculares

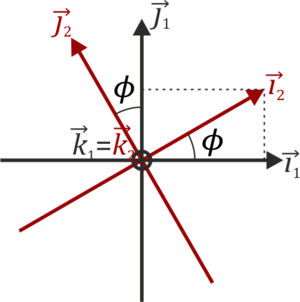
Sea ϕ el ángulo que forma el aro intermedio (“sólido 2”) con el exterior (“sólido 1”), y θ el que el aro interior (“sólido 3”) forma con el intermedio. Cuando los dos ángulos se anulan los tres aros son coplanarios. Puede asociarse un sistema de ejes a cada sólido, de manera que el eje de las rotaciones en ϕ es $O Z 1 = O Z 2$ y el de las de θ es $O X 2 = O X 3$ . En función de los dos ángulos y sus derivadas respecto al tiempo

Indique las relaciones entre las bases ligadas a cada sólido
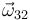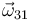Exprese las velocidades angulares $\vec{\omega}_{21}$ , $\vec{\omega}_{32}$ y $\vec{\omega}_{31}$ .
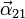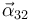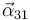Exprese las aceleraciones angulares $\vec{\alpha}_{21}$ , $\vec{\alpha}_{32}$ y $\vec{\alpha}_{31}$ .

2 Relaciones entre bases

2.1 Entre la base 1 y la 2

El giro se realiza alrededor del eje $O Z 1$ , por lo que el vector en la dirección de este eje es el mismo en las dos bases

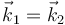
$\vec{k}_1=\vec{k}_2$

mientras que los otros 2 se calculan mediante una rotación de un ángulo ϕ. Esto nos da las relaciones

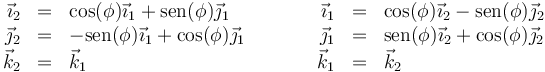
$\begin{array}{rclcrcl} \vec{\imath}_2&=&\cos(\phi)\vec{\imath}_1+\mathrm{sen}(\phi)\vec{\jmath}_1&\qquad&\vec{\imath}_1&=&\cos(\phi)\vec{\imath}_2-\mathrm{sen}(\phi)\vec{\jmath}_2\\ \vec{\jmath}_2&=&-\mathrm{sen}(\phi)\vec{\imath}_1+\cos(\phi)\vec{\jmath}_1&\qquad&\vec{\jmath}_1&=&\mathrm{sen}(\phi)\vec{\imath}_2+\cos(\phi)\vec{\jmath}_2\\ \vec{k}_2&=&\vec{k}_1&\qquad&\vec{k}_1&=&\vec{k}_2 \end{array}$

2.2 Entre la base 2 y la 3

De la misma manera obtenemos la relación entre la base intermedia 2 y la interior, 3. En este caso el giro es en torno al eje $O X 2$ or lo que el vecor en esta dirección no se ve afectado

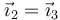
$\vec{\imath}_2=\vec{\imath}_3$

mientras que los otros dos se relacionan mediante la rotación correspondiente. Esto da

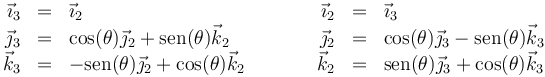
$\begin{array}{rclcrcl} \vec{\imath}_3&=&\vec{\imath}_2&\qquad&\vec{\imath}_2&=&\vec{\imath}_3\\ \vec{\jmath}_3&=&\cos(\theta)\vec{\jmath}_2+\mathrm{sen}(\theta)\vec{k}_2&\qquad&\vec{\jmath}_2&=&\cos(\theta)\vec{\jmath}_3-\mathrm{sen}(\theta)\vec{k}_3\\ \vec{k}_3&=&-\mathrm{sen}(\theta)\vec{\jmath}_2+\cos(\theta)\vec{k}_2&\qquad&\vec{k}_2&=&\mathrm{sen}(\theta)\vec{\jmath}_3+\cos(\theta)\vec{k}_3 \end{array}$

3 Velocidades angulares

Del movimiento {21}

Al ser el eje de giro el $O Z 1$ la velocidad angular de este movimiento en

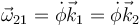
$\vec{\omega}_{21}=\dot{\phi}\vec{k}_1=\dot{\phi}\vec{k}_2$

Del movimiento {32}

De la misma manera

$\vec{\omega}_{32}=\dot{\theta}\vec{\imath}_2=\dot{\imath}\vec{\imath}_3$

Del movimiento {31}

Este es composición de los dos anteriores

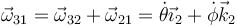
$\vec{\omega}_{31}=\vec{\omega}_{32}+\vec{\omega}_{21}=\dot{\theta}\vec{\imath}_2+\dot{\phi}\vec{k}_2$

En este caso, la expresión más simple de la velocidad angular se tiene en la base intermedia “2”. Sin embargo, puede ser necesario expresarla en el sistema fijo 1 o en e ligado 3. Para ello, empleamos las relaciones entre bases, expresadas en la sección anterior. En la bae fija

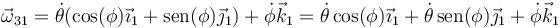
$\vec{\omega}_{31}=\dot{\theta}(\cos(\phi)\vec{\imath}_1+\mathrm{sen}(\phi)\vec{\jmath}_1)+\dot{\phi}\vec{k}_1=\dot{\theta}\cos(\phi)\vec{\imath}_1+\dot{\theta}\,\mathrm{sen}(\phi)\vec{\jmath}_1+\dot{\phi}\vec{k}_1$

y en la ligada al sólido 3

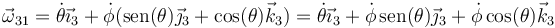
$\vec{\omega}_{31}=\dot{\theta}\vec{\imath}_3+\dot{\phi}(\mathrm{sen}(\theta)\vec{\jmath}_3+\cos(\theta)\vec{k}_3)=\dot{\theta}\vec{\imath}_3+\dot{\phi}\,\mathrm{sen}(\theta)\vec{\jmath}_3+\dot{\phi}\cos(\theta)\vec{k}_3$

4 Aceleraciones angulares

Del movimiento {21}

Al ser el eje de giro $O Z 1$ un eje permanente la aceleración angular de este movimiento en

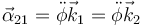
$\vec{\alpha}_{21}=\ddot{\phi}\vec{k}_1=\ddot{\phi}\vec{k}_2$

Del movimiento {32}

De la misma manera

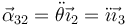
$\vec{\alpha}_{32}=\ddot{\theta}\vec{\imath}_2=\ddot{\imath}\vec{\imath}_3$

Del movimiento {31}

Este es composición de los dos anteriores

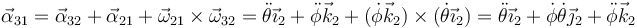
$\vec{\alpha}_{31}=\vec{\alpha}_{32}+\vec{\alpha}_{21}+\vec{\omega}_{21}\times\vec{\omega}_{32}=\ddot{\theta}\vec{\imath}_2+\ddot{\phi}\vec{k}_2+(\dot{\phi}\vec{k}_2)\times(\dot{\theta}\vec{\imath}_2)= \ddot{\theta}\vec{\imath}_2+\dot{\phi}\dot{\theta}\vec{\jmath}_2+\ddot{\phi}\vec{k}_2$

De nuevo, si es preciso, puede pasarse esta aceleración angular a la base fija o a la base ligada, mediante el cambio de base correspondiente.

Suspensión cardán de dos ejes (CMR)

De Laplace

Contenido

1 Enunciado

2 Relaciones entre bases

2.1 Entre la base 1 y la 2

2.2 Entre la base 2 y la 3

3 Velocidades angulares

4 Aceleraciones angulares

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES