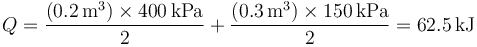Solución de la 1ª convocatoria 12/13 (2ª parte)(GIE)
De Laplace
Contenido |
1 Preguntas T.1, T.2 y T.3
Se tiene una cierta cantidad de aire en un cilindro con paredes adiabáticas y con un pistón también adiabático, que puede moverse pero permanece en reposo, situado en un ambiente a presión p0 y temperatura T0. Al retirar el aislamiento térmico del cilindro, se encuentra que el pistón comprime el gas.

1.1 Pregunta T.1
Antes de retirar el aislamiento, ¿había equilibrio entre el aire y el ambiente?
- A. No había equilibrio ni térmico ni mecánico.
- B. Había equilibrio mecánico, pero no térmico.
- C. Había equilibrio térmico, pero no mecánico.
- D. Había equilibrio tanto térmico como mecánico.
1.1.1 Solución
La respuesta correcta es la B.
Si el émbolo era libre de moverse, pero no lo hacía es porque la fuerza sobre él era nula, es decir, el sistema se encontraba en equilibrio mecánico.
Por otro lado, al retirar el aislamiento térmico se produjo un intercambio de energía entre el sistema y el entorno. Por tanto su temperatura no podía ser la misma que la del exterior, ya que hubo transferencia de calor.
Por tanto, había equilibrio mecánico, pero no térmico y la respuesta correcta es la B.
1.2 Pregunta T.2
¿Qué podemos decir de la temperatura inicial del gas, Ti?
- A. Ti = T0
- B. No podemos saber nada de la temperatura inicial.
- C. Ti > T0
- D. Ti < T0
1.2.1 Solución
La respuesta correcta es la C.
La presión inicial y la final del gas es la misma e igual a la exterior, por lo que la ley de los gases ideales se reduce a la ley de Charles
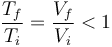
Puesto que el volumen se reduce, también lo hace la temperatura. Por tanto, su temperatura inicial era mayor que la final, que es la del exterior
1.3 Pregunta T.3
- ¿Cómo es la variación de entropía del gas interior entre el estado inicial y el final?
- A. Puede tener cualquier signo.
- B. ΔS > 0
- C. ΔS = 0
- D. ΔS < 0
1.3.1 Solución
La respuesta correcta es la D.
Si la temperatura del gas disminuye manteniéndose la presión constante, es porque sale calor del sistema. Por tanto, la entropía del gas disminuye.
Si queremos una fórmula, puesto que la presión es constante, sería
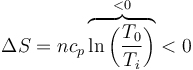
2 Pregunta T.4
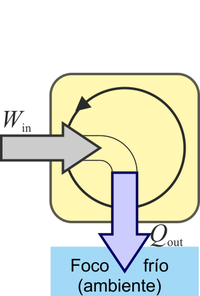
¿Cuál de las siguientes procesos está prohibido explícitamente por el enunciado de Kelvin-Planck del segundo principio de la termodinámica?
| 
|
| A | B |
|---|---|

| 
|
| C | D |
2.1 Solución
La respuesta correcta es la B.
El enunciado de Kelvin-Planck es:
Es imposible construir una máquina que, operando en un ciclo, produzca como único efecto la extracción de calor de un foco y la realización de una cantidad equivalente de trabajo
Puesto que el enunciado de Clausius es equivalente al de Kelvin-Planck, éste también prohíbe el caso D, pero no lo hace explícitamente.
es decir, que lo que prohíbe es que se absorba calor de un foco (el llamarlo frío o caliente es irrelevante, pues solo hay uno) y ese calor se transforme en trabajo.
3 Pregunta T.5
¿Cuál de las siguientes curvas corresponde a un ciclo de Carnot en un diagrama TS?

| 
|
| A | B |
|---|---|

| 
|
| C | D |
3.1 Solución
La respuesta correcta es la D.
Un ciclo de Carnot está formado por dos isotermas y dos adiabáticas. En un diagrama TS una isoterma es una recta horizontal. Un proceso adiabático reversible es un proceso isentrópico, por lo que su gráfica es una línea vertical. Por tanto el ciclo de Carnot, como se ha estudiado en el curso, es un rectángulo.
4 Pregunta T.6
Un bloque de aluminio de 4 kg a 80°C se coloca sobre un gran bloque de hielo a 0°C. ¿Cuánto hielo se derrite, aproximadamente? (calor específico del aluminio: 0.897 kJ/(kg·K); calor específico del agua: 4.18kJ/(kg·K); entalpía específica de fusión del agua: 333.55 kJ/kg)
- A. 215 g
- B. 11 g
- C. 4.0 kg
- D. 860 kg
4.1 Solución
La respuesta correcta es la D.
Al poner en contacto el aluminio con el hielo, se produce una transferencia de calor del más caliente al más frio. Como resultado, la temperatura del aluminio comienza a descender. En el hielo, en cambio, el efecto es un cambio de estado, pasando de hielo a 0°C a agua a 0°C. El calor que sale del aluminio es
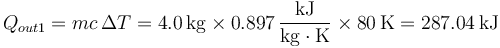
Este calor se emplea en fundir una masa M de hielo, de forma que
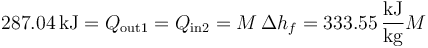
Despejando de aquí

5 Preguntas T.7 y T.8
Un gas ideal diatómico experimenta un proceso cuasiestático desde un estado A a un estado B, según la gráfica de la figura
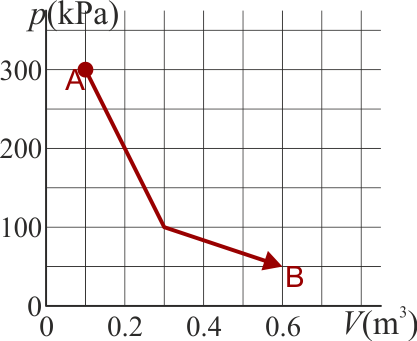
5.1 Pregunta T.7
¿Cuánto es la variación de la energía interna del gas?
- A. Es nula.
- B. No podemos conocerlo sin saber el número de moles.
- C. −53.7kJ
- D. +62.5kJ
5.1.1 Solución
La respuesta correcta es la A.
La variación de energía interna en el gas puede calcularse mediante la expreisón

por lo que determinar es cómo varía la temperatura o el producto pV. Ahora bien, tenemos que, en el estado inicial
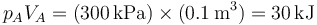
y en el final
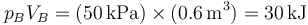
es decir, la temperatura inicial y la final son la misma, por lo que
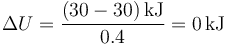
5.2 Pregunta T.8
¿Cuánto calor entra en el gas en este proceso?
- A. +53.7kJ
- B. No podemos conocerlo sin saber el número de moles.
- C. −53.7kJ
- D. +62.5kJ
5.2.1 Solución
La respuesta correcta es la D.
Calculamos el calor aplicando el primer principio de la termodinámica
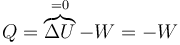
A su vez, el trabajo lo calculamos a partir de la integral de la presión

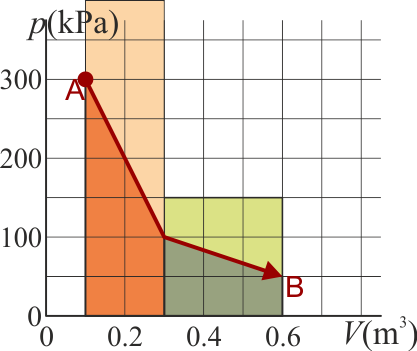
El área bajo la curva es la suma de dos trapecios. Su valor puede hallarse o bien aplicando la fórmula del área de un trapecio u observando que cada uno es la mitad de un rectángulo. Por ello