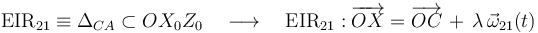Rotación instantánea de Sólido Rígido: aplicación, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Movimiento del cilindro respecto del tronco de cono
  - 2.1.1 Propiedades de la reducción cinemática
- 2.2 Eje instantaneo de rotación

1 Enunciado

Un cilindro recto de radio

R

en sus bases y altura

2 R

(sólido “2”), se mueve respecto de un tronco de cono (sólido “1”), cuyas bases son sendos círculos de radios

R

y

2 R

, y cuya generatriz tiene una longitud

2 R

. El movimiento es tal que, en cada instante, los sólidos “1” y “2” tienen en contacto una generatriz $\overline{AB}$ , y la base superior del cilindro rueda sin deslizar sobre el perímetro de la base pequeña del tronco de cono. Justifique por qué el movimiento

{21}

es una rotación instantánea e indique razonadamente qué puntos forman el eje instantáneo de rotación de dicho movimiento.

2 Solución

El movimiento de un sólido “2” respecto de otro considerado fijo (sólido “1”) es una rotación instantánea cuando, en un determinado instante, todos los puntos de aquél realizan sendos movimientos circulares, en torno al mismo eje, denominado eje instantáneo de rotación.

La reducción cinemática en un punto arbitrario $P$ del sólido “2”, para un movimiento de rotación instantánea ${21}$ , se caracteriza porque sus elementos verifican las siguientes propiedades generales:

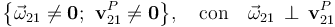
$\big\{\vec{\omega}_{21}\neq\mathbf{0}\mathrm{;}\;\;\mathbf{v}_{21}^P\neq\mathbf{0}\big\}\mathrm{,}\,\quad\mathrm{con}\quad\vec{\omega}_{21}\!\ \perp\!\ \mathbf{v}_{21}^P$

En consecuencia, la velocidad mínima correspondiente a un movimiento instantáneo de rotación es,

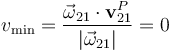
$v_\mathrm{min}=\frac{\vec{\omega}_{21}\cdot\mathbf{v}_{21}^P}{|\vec{\omega}_{21}|}=0$

y, por tanto, existen puntos del sólido “2” que se encuentran en reposo instantáneo. Como se sabe, dichos puntos están alineados a lo largo de una recta paralela al vector rotación instantánea $\vec{\omega}_{21}$ , constituyendo el eje instantáneo de rotación, $EIR 21$ :

$\mathbf{v}_{21}^I=\mathbf{0}\quad\Longleftrightarrow\quad I\in\mathrm{EIR}_{21}\!\ \|\!\ \vec{\omega}_{21}$

Así, la reducción cinemática canónica que describe un movimiento instantáneo de rotación es de la forma,

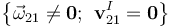
$\big\{\vec{\omega}_{21}\neq\mathbf{0}\mathrm{;}\;\;\mathbf{v}_{21}^I=\mathbf{0}\big\}$

Por otra parte, el carácter instantáneo del movimiento se manifiesta en que, aunque el sólido realizase también una rotación pura en todo instante, los puntos en reposo instantáneo (es decir, el eje instantáneo de rotación) cambiarían durante el movimiento.

2.1 Movimiento del cilindro respecto del tronco de cono

2.1.1 Propiedades de la reducción cinemática

Según se describe en el enunciado, el cilindro (sólido “2”) se mueve de manera que, en todo instante, el perímetro de una de sus bases rueda sin deslizar el contorno de la base menor del tronco de cono fijo (sólido “1”). Esto implica que el punto del sólido “2” que coincide con la posición $A$ indicada en la figura, se encuentra en reposo instantáneo, por lo que si realizamos la reducción cinemática instantánea del movimiento ${21}$ en dicho punto $A$ , se tendrá que uno de los elementos de dicha reducción es

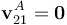
$\mathbf{v}_{21}^A=\mathbf{0}$

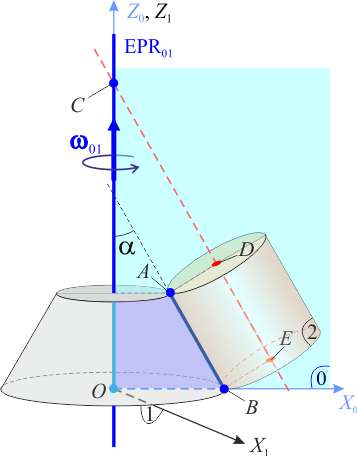
Luego, para justificar que dicho movimiento es una rotación instantánea debemos comprobar que el vector rotación $\vec{\omega}_{21}$ es no nulo y que el eje instantáneo de rotación $EIR 21$ cambia durante el movimiento. Para obtener dichas propiedades resulta conveniente introducir un sistema de referencia auxiliar $O X 0 Y 0 Z 0$ (sólido “0”) que nos permita descomponer el movimiento bajo estudio en otros más sencillos. Elegimos el sólido “O” de manera que el eje $O Z 0$ coincida en todo instante con el eje de simetría $O Z 1$ del sólido “1”, y que el plano $O X 0 Z 0$ contenga siempre al segmento $\overline{AB}$ , coincidente en cada instante con las generatrices del cilindro y del tronco de cono que se hallan en contacto. Obsérvese que, con estas condiciones, el eje de simetría del cilindro (el que pasa por los puntos $D$ y $E$ ) también va a estar siempre contenido en el plano $O X 0 Z 0$ . 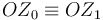Por tanto, cuando el cilindro se mueve respecto del tronco de cono, aquel plano realiza una rotación permanente alrededor del eje fijo $O Z 1$ , en la cuál los puntos del eje $O Z 0$ permanecen siempre en reposo al ser $OZ_0\equiv OZ_1$ . Si se adopta el punto $O$ como centro de reducción para describir el movimiento ${01}$ , la correspondiente reducción cinemática va a ser de la forma:

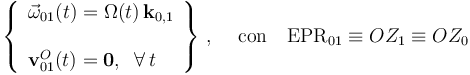
$\left\{\begin{array}{l}\displaystyle\vec{\omega}_{01}(t)=\Omega(t)\!\ \mathbf{k}_{0\mathrm{,}1}\\ \\ \mathbf{v}_{01}^O(t)=\mathbf{0}\mathrm{,}\,\;\;\forall\, t\end{array}\right\}\,\mathrm{,}\,\quad\,\mathrm{con}\quad\mathrm{EPR}_{01}\equiv OZ_1\equiv OZ_0$

y donde $Ω(t)$ es una ley horaria sobre la que no se dan datos en el enunciado, pero que será distinta de cero, en general. Su expresión dependerá de la forma en que el segmento $\overline{AB}$ , coincidente con las generatrices de contacto, recorra la superficie del tronco de cono.

Nótese que cuando el cilindro (sólido “2”) se mueve sobre el tronco de cono (sólido “1”), los puntos de ambos sólidos que se hallan en contacto (coincidentes con el segmento $\overline{AB}$ ), van cambiado durante el transcurso de dicho movimiento. Por tanto, aunque el segmento $\overline{AB}$ ocupa una posición fija en el plano $O X 0 Z 0$ , los puntos del sólido “2” que en un cierto instante se hallan en esa posición, en general no van a estar en reposo respecto del plano $O X 0 Z 0$ . Por ejmeplo, en el caso particular del punto $A$ , en el cuál el cilidro rueda sin deslizar sobre la base superior del tronco de cono, se tendrá:

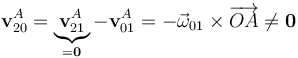
$\mathbf{v}_{20}^A=\underbrace{\mathbf{v}_{21}^A}_{=\mathbf{0}}-\mathbf{v}_{01}^A=-\vec{\omega}_{01}\times\overrightarrow{OA}\neq\mathbf{0}$

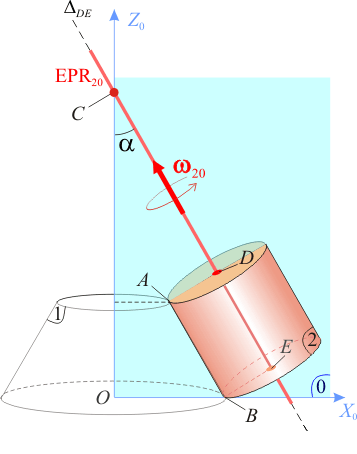
Sin embargo, existe un conjunto de puntos que sí se encuentran en reposo permanente en el movimiento ${20}$ : los puntos del cilindro que se encuentran en el eje $Δ D E$ que pasa por $D$ y $E$ . Éstos ocupan posiciones fijas en el plano $O X 0 Z 0$ , por lo que se verifica:

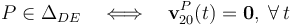
$P\in \Delta_{DE}\quad\Longleftrightarrow\quad \mathbf{v}_{20}^P(t)=\mathbf{0}\mathrm{,}\,\;\forall\,t$

En consecuencia, la reducción cinemática que caracteriza al movimiento ${20}$ es:

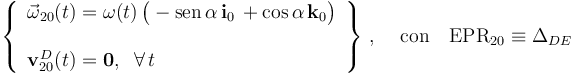
$\left\{\begin{array}{l}\displaystyle\vec{\omega}_{20}(t)=\omega(t)\!\ \big(-\mathrm{sen}\,\alpha\!\ \mathbf{i}_0\!\ +\cos\alpha\!\ \mathbf{k}_{0}\big)\\ \\ \mathbf{v}_{20}^D(t)=\mathbf{0}\mathrm{,}\,\;\;\forall\, t\end{array}\right\}\,\mathrm{,}\,\quad\,\mathrm{con}\quad\mathrm{EPR}_{20}\equiv \Delta_{DE}$

donde $α$ es el ángulo constante que forma el eje $Δ D E$ con la dirección vertical, y $ω(t)$ es la ley horaria horaria que describe cómo gira el sólido alrededor de aquél eje, y que va a estar determinada por la condición de rodar sin deslizar en el punto $A$ del sólido “2” y por la ley $Ω(t)$ que describe la rotación del plano $O X 0 Z 0$ alrededor del eje $O Z 1$ :

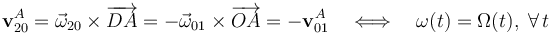
$\mathbf{v}_{20}^A=\vec{\omega}_{20}\times\overrightarrow{DA}=-\vec{\omega}_{01}\times\overrightarrow{OA}=- \mathbf{v}_{01}^A\quad\Longleftrightarrow\quad \omega(t)=\Omega(t)\mathrm{,}\,\;\forall\,t$

Una vez que tenemos las reducciones cinemáticas correspondientes a los movimientos ${01}$ y ${20}$ , las leyes para la composición de movimientos, permiten determinar la propiedad que nos faltaba conocer a cerca del movimiento absoluto ${21}$ :

$\vec{\omega}_{21}(t)=\vec{\omega}_{20}(t)+\vec{\omega}_01(t)=\Omega(t)\!\ \big[-\mathrm{sen}\,\alpha\!\ \mathbf{i}_0(t)\!\ +(1+\cos\alpha)\!\ \mathbf{k}_{1}\big]$

Obsérvese que con tal de que el cilindro se esté moviendo en torno al eje vertical $O Z 1$ , la función $Ω(t)$ tendrá un valor no nulo y las características de la reducción cinemática instantánea del movimiento ${21}$ en el punto del cilindro que ocupa la posición $A$ , serán

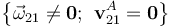
$\big\{\vec{\omega}_{21}\neq\mathbf{0}\mathrm{;}\;\;\mathbf{v}_{21}^A=\mathbf{0}\big\}$

que, como discutimos al principio, se corresponde con una rotación pura del sólido alrededor de un eje que pasa por $A$ y tiene la dirección paralela a $\vec{\omega}_{21}$ . Para justificar que este movimiento tiene carácter instantáneo, comprobamos que la posición del eje de rotación respecto del sólido fijo, cambia durante el transcurso del movimiento: en cada instante, el $EIR 21$ pasa por el punto del sólido “2” que ocupa la posición $A$ , y ésta va moviéndose sobre el contorno de la base menor del tronco de cono (sólido “1”).

2.2 Eje instantaneo de rotación

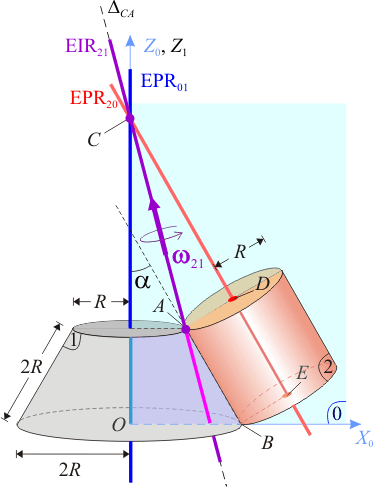
La localización del

EIR 21

en cada instante puede determinarse fácilmente: al tratarse de un movimiento de rotación pura, el eje de rotación pasa por todos aquellos puntos que se encuentran en reposo instantáneo. Por tanto, basta con determinar dos puntos del sólido “2” en dicha situación para saber la posición del

EIR 21

. Conocemos uno de ellos: el punto que ocupa la posición

A

. Otro es el punto virtual del sólido “2” que ocupa la posición

C

. Obsérvese que dicho punto es la intersección del eje

O Z 0

del sólido “0” con el eje

Δ D E

. Y como éstos son los ejes permanentes de rotación de los movimientos

{01}

y

{20}

, respectivamente, se tendrá que el punto

C

se hallaría en resposo permanente en el movimiento

{21}

: $C=\mathrm{EPR}_{01}\bigcap\mathrm{EPR}_{20}\quad\Longrightarrow\quad\left\{\begin{array}{l}\mathbf{v}_{01}^C(t)=\mathbf{0}\\ \\ \mathbf{v}_{20}^C(t)=\mathbf{0}\end{array}\right\}\,\Longrightarrow\quad\mathbf{v}_{21}^C(t)=\mathbf{0}\mathrm{,}\,\;\forall\, t$

Por tanto, en cada instante de tiempo, el eje instantáneo de rotación del movimiento ${21}$ coincide con el eje $Δ A C$ que pasa por los puntos $C$ y $A$ . En consecuencia, este eje esta contenido en cada instante plano $O X 0 Z 0$ que, como vimos en el partado anterior, gira alrededor del eje $O Z 1$ cuando el cilindro se mueve sobre el tronco cono:

$\mathrm{EIR}_{21}\equiv\Delta_{CA}\subset OX_0Z_0\quad\longrightarrow\quad\mathrm{EIR}_{21}:\overrightarrow{OX}=\overrightarrow{OC}\!\ +\!\ \lambda\!\ \vec{\omega}_{21}(t)$

Rotación instantánea de Sólido Rígido: aplicación, F1 GIA (Sept, 2012)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Movimiento del cilindro respecto del tronco de cono

2.1.1 Propiedades de la reducción cinemática

2.2 Eje instantaneo de rotación

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES