Rectas de regresión

De Laplace

Contenido

1 Introducción
2 Antes de hacer ningún cálculo: gráfica de los puntos
- 2.1 Ejes e intervalos en una gráfica
- 2.2 Ubicación
3 Coeficiente de correlación

1 Introducción

En numerosas ocasiones no debemos determinar cuánto vale una cantidad directa o indirectamente, sino cómo depende una variable de otra.

A la hora de establecer una dependencia vamos variando una cierta magnitud $x$ (a la que denominaremos entrada}) en una serie de valores $x i$ . Para cada uno de estos valores medimos un valor $y i$ de una magnitud $y$ (la respuesta o salida). El resultado puede tabularse en una tabla de dos columnas, y representarse gráficamente.

Ejemplo: Supongamos que fijamos la tensión en los extremos de un cable y medimos la corriente que circula por él, obteniendo el siguiente resultado

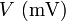
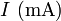
$V\ (\mathrm{mV})$	$I\ (\mathrm{mA})$
3.25	1.40
3.50	2.93
3.75	3.28
4.00	4.30
4.25	11.92
4.50	6.65
4.75	8.57
5.00	9.56
5.25	11.58
5.50	13.61
5.75	15.64

Es evidente, de este comportamiento, que existe una relación funcional entre $x$ e $y$ ( $I$ y $V$ en este caso). Ahora bien, ¿qué función representa correctamente esta conducta, una recta, una parábola, una exponencial? Y, si se trata de una parábola, ¿cuáles son los coeficientes $a$ , $b$ , $c$ de la función $y = a x 2 + b x + c$ ?

Además, sospechamos que el punto que se aparta mucho del resto es un error experimental y no debe ser tenido en cuenta. Sin embargo, ¿cómo podemos estar seguros de ello? Quizás la dependencia entre $x$ e $y$ sea muy compleja y el punto separado sea correcto.

Este tipo de problema se denomina ajuste de una función y como vemos puede ser extremadamente complicado, dependiendo del tipo de función y del número de datos y parámetros empleados para describirla.

Aquí nos limitaremos al caso más simple: el ajuste de una recta por el método de mínimos cuadrados. Partimos de una serie de datos más o menos alineados y trataremos de buscar la recta que pasa más cerca de ellos.

Este tipo de ajuste es de interés en varias situaciones diferentes

Cuando tenemos una serie de entradas y salidas, para las cuales no sabemos si existe una relación funcional, pero lo sospechamos, como en la figura anterior. En este caso, la bondad de la recta de regresión (esto es, cuánto se aproxima a los datos) nos informa de si esta relación existe o no.
Cuando tenemos un conjunto de datos, de los cuales sabemos con seguridad que deberían estar alineados y queremos emplear la recta de mejor ajuste para determinar alguna cantidad indirecta. Por ejemplo, supongamos que conocemos una serie de pares de valores de tensión $V$ frente a intensidad de corriente $I$ para un cable y queremos determinar la resistencia de acuerdo con la ley de Ohm, $V = I R$ . En lugar de determinar una resistencia para cada dato, buscaremos la recta de mejor ajuste, cuya pendiente será la resistencia buscada.
Las rectas de mejor ajuste también pueden usarse para hallar el valor de la salida para entradas que no hayamos medido experimentalmente. Esto es lo que se conoce como interpolación si $x$ se encuentra en el mismo intervalo que los datos experimentales y extrapolación si está fuera de éste.
Cuando tenemos un conjunto de datos para los cuales existe una relación funcional complicada, como la ilustrada en la figura, pero para la cual sabemos que en determinadas regiones, más o menos grandes, la conducta es aproximadamente lineal. En este caso, si nos restringimos a una de estas regiones, podemos aproximar la función por la recta de mejor ajuste, lo que simplifica los cálculos. Por supuesto, en este caso la recta de mejor ajuste dependerá de la región en que nos encontremos, por lo que deberemos ser conscientes en todo momento de los límites de validez de la aproximación que empleemos. En estas aproximaciones también podemos emplear la recta de mejor ajuste para interpolar. Sin embargo, las extrapolaciones son mucho más arriesgadas, ya que podemos salirnos de los límites de validez.

El cálculo de la recta de mínimos cuadrados es inseparable del trazado de la gráfica correspondiente.

2 Antes de hacer ningún cálculo: gráfica de los puntos

Antes incluso de determinar la pendiente y la ordenada en el origen de la recta de mejor ajuste, podemos establecer si los puntos están más o menos alineados.

Para ello, antes de hacer ningún cálculo, situamos los puntos en una gráfica, sea por ordenador o sobre papel milimetrado. Una simple inspección de su posición nos indicará si es conveniente ajustar una recta, si necesitáramos una función más complicada o si no se ve ninguna relación entre las entradas y las salidas. Igualmente en esta fase podemos descartar algún punto que se aparte excesivamente del resto. En este caso, dicho punto no se incluirá en los cálculos, aunque si debe indicarse en la gráfica. Debe rodearse por un pequeño círculo, como indicación de que no ha sido considerado.

Aplicando esto a nuestra lista de datos, eliminamos el punto 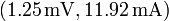$(1.25\,\mathrm{mV}, 11.92\,\mathrm{mA})$ , que en lo sucesivo no será incluido en los cálculos, salvo que indiquemos lo contrario.

La nube de puntos resultantes quedaran cubiertos por una elipse (que no hay que trazar). Los puntos estarán tanto más alineados cuanto más se aproxima esta elipse a una recta, esto es, cuanto más ``estrecha es.

2.1 Ejes e intervalos en una gráfica

La representación de una serie de datos deberá hacerse de forma que los puntos ocupen el máximo posible de papel. Para ello se elegirán los intervalos desde ligeramente por debajo del dato menor a un poco por encima del dato mayor. Así, para la tabla anterior, intervalos posibles serían de 3 mV a 6 mV para las $x$ y de 0 mA a 16 mA para las $y$ . No importa que el origen de coordenadas quede fuera de la gráfica, ni que los intervalos de cada escala tengan diferente extensión.

Los ejes se dividirán en segmentos adecuados, de forma que haya 5 ó 6 en cada uno (en nuestro caso podrían ser de 0.5 mV en 0.5 mV en las $x$ y de 2.5 mA en 2.5 mA en las $y$ ). No obstante, debe procurarse que las escalas y sus divisiones sean “normales”, en cuanto a que puede dividirse una unidad en medios o en cuartos, pero no es normal dividirla en séptimos, por ejemplo.

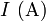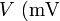En los extremos de los ejes se indicarán las magnitudes y las unidades en las que mide entre paréntesis, ( $I\ (\mathrm{A})$ y $V\ (\mathrm{mV}$ ) en este caso).

No hay que escribir las coordenadas de los datos, ni en los ejes ni cerca de cada punto. Esto es redundante y dificulta la observación de la gráfica.

2.2 Ubicación

Las gráficas que se hagan, sean exclusivamente de los datos experimentales, de rectas de mínimos cuadrados, u otras solicitadas explícitamente, deben adjuntarse al final de la memoria, estando convenientemente etiquetadas.

Toda gráfica deberá ir numerada y con un título explicativo. Si hay varias curvas o rectas trazadas en la misma hoja se indicará cuál es cada una.

3 Coeficiente de correlación

Como medida matemática del grado de alineación (o correlación lineal), la magnitud relevante es el llamado coeficiente de correlación lineal, $r$ , definido como

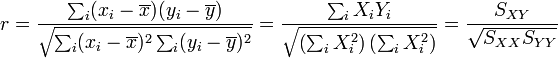
$r = \frac{\sum_i (x_i-\overline{x})(y_i-\overline{y})}{\sqrt{\sum_i (x_i-\overline{x})^2\sum_i (y_i-\overline{y})^2}} = \frac{\sum_i X_iY_i}{\sqrt{\left(\sum_i X_i^2\right)\left(\sum_i X_i^2\right)}} = \frac{S_{XY}}{\sqrt{S_{XX}S_{YY}}}$

Esta definición es análoga a la medida de la correlación entre dos variables, definida al estudiar el error de una función de varias variables, con la única diferencia de que aquella se supone calculada conocida la distribución completa (esto es, infinitos datos), mientras que ésta se limita a los datos de que disponemos.

A partir de esta definición puede demostrarse que el coeficiente de correlación es una cantidad comprendida en el intervalo $( - 1,1)$ , siendo su signo el mismo de la pendiente de la recta de mejor ajuste (positivo si la recta va hacia arriba y negativo en caso contrario).

Podemos caracterizar la alineación dividiendo los valores de $r$ en intervalos:

|r|=+1: Los puntos se encuentran perfectamente alineados.
0.75<|r|<1: Los puntos muestran una clara alineación, que será mejor cuanto más se acerque $r$ a la unidad.
0.25<|r|<0.75: Existe una cierta tendencia lineal entre los puntos, que disminuye al reducirse $r$ .
0<|r|<0.25: No puede decirse que exista una relación lineal entre $x$ e $y$ , ya que los puntos forman una nube casi informe.
|r|=0: no existe correlación entre la entrada y la salida, esto es, se trata de variables independientes entre sí.

Ejemplo: En el caso que estamos considerando obtenemos

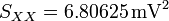
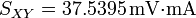
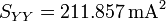
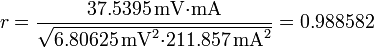
$S_{XX}=6.80625\,\mathrm{mV}^2$ $S_{XY} = 37.5395\,\mathrm{mV}{\cdot}\mathrm{mA}$ $S_{YY} = 211.857\,\mathrm{mA}^2$ $r = \frac{37.5395\, \mathrm{mV}{\cdot}\mathrm{mA}}{\sqrt{6.80625\,\mathrm{mV}^2{\cdot}211.857\, \mathrm{mA}^2}} = 0.988582$

Vemos que resulta una cantidad adimensional próxima a la unidad, lo que indica el hecho ya conocido a partir de la gráfica de que los datos están muy alineados.

Las calculadoras que incluyen cálculos de regresión o las hojas de cálculo, como Excel, incorporan entre sus funciones el coeficiente de correlación, con lo que basta introducir los datos y aplicar dicha función.

Caso de que esto no sea posible, puede recurrirse a la definición indicada antes, o a la expresión matemáticamente equivalente

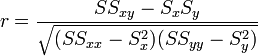
$r = \frac{SS_{xy}-S_xS_y}{\sqrt{(SS_{xx}-S_x^2)(SS_{yy}-S_y^2)}}$

donde

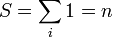
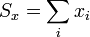
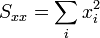
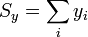
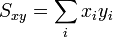
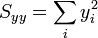
$S=\sum_i 1 = n\,$ $S_x = \sum_i x_i\,$ $S_{xx} = \sum_i x_i^2\,$ $S_y = \sum_i y_i\,$ $S_{xy} = \sum_i x_iy_i\,$ $S_{yy} = \sum_i y_i^2\,$

Aunque teóricamente esta expresión da el mismo resultado que la definición, es posible que al calcularla en un ordenador o calculadora, se obtenga un valor diferente, debido a la presencia de errores de redondeo, como los que se comentan al estudiar la incertidumbre debido a varias medidas de la misma magnitud. Por ello, si esta operación se hace con una hoja de cálculo, es preferible emplear la definición, con los valores medidos respecto a la media, tal como aparece en la ecuación dada inicialmente, que presenta un menor error.

El coeficiente de correlación es una propiedad de la distribución de la nube de puntos y no es preciso hallar el error de esta cantidad (que se debería a la incertidumbre de cada dato). Al no disponer de un error para truncar las cifras significativas, adoptaremos el criterio de retener todos los 9's consecutivos que haya tras el punto decimal, más la primera cifra distinta de 9 que les siga, sin redondear esta última cifra. Por ejemplo, si $r = 0.999816$ lo redondeamos a $r = 0.9998$ , si $r = 0.994923$ lo dejamos en $r = 0.994$ y si $r = 0.989$ como $r = 0.98$ . La razón de este extraño convenio es que estamos más interesados en ver cuánto se aproxima $r$ a la unidad, como medida de buena alineación, por lo que la información más significativa es la cantidad de $9$ 's que hay tras el punto decimal. En nuestro ejemplo sería $r = 0.98$ .

Un coeficiente de correlación bajo para una lista de puntos en la que sabemos con seguridad que debería existir una relación lineal sugiere que existe algún dato aislado que se separa del resto. La gráfica de estos puntos, como indicamos en la sección anterior, puede decirnos si debemos descartar algún dato, lo que suele redundar en la mejora del valor de $r$ (esto es, que se acercará más a la unidad). Así, en nuestro ejemplo, si hubiéramos retenido el dato que hemos descartado, habría resultado un valor de $r = 0.922556$ , mientras que sin él resulta $r = 0.988582$ , como ya hemos visto.

Rectas de regresión

De Laplace

Contenido

1 Introducción

2 Antes de hacer ningún cálculo: gráfica de los puntos

2.1 Ejes e intervalos en una gráfica

2.2 Ubicación

3 Coeficiente de correlación

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES