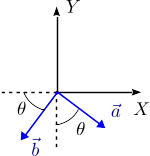
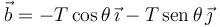Proyección de un vector y otro perpendicular a él
De Laplace
Contenido |
1 Enunciado
En estas cuatro configuraciones el vector  es perpendicular al vector
es perpendicular al vector  . Los dos tienen módulo T. Encuentra la expresión de los cuatro vectores en los ejes cartesianos mostrados.
. Los dos tienen módulo T. Encuentra la expresión de los cuatro vectores en los ejes cartesianos mostrados.
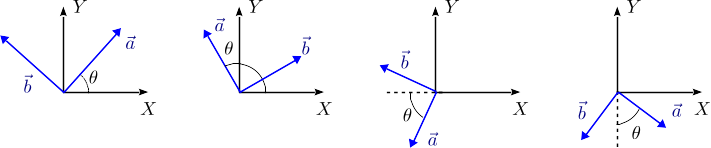
1.1 Caso a
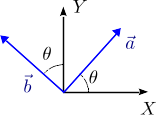
El vector  forma un ángulo θ con el eje + X. Entonces
forma un ángulo θ con el eje + X. Entonces
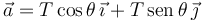
En el dibujo se muestra el ángulo que forma el vector  con el eje + Y. Entonces
con el eje + Y. Entonces
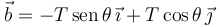
1.2 Caso b
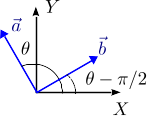
El vector  forma un ángulo θ con el eje + X. Entonces
forma un ángulo θ con el eje + X. Entonces
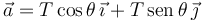
Hay que señalar que no hay que imponer ningún signo negativo en las componentes. El propio coseno da el signo adecuado en cada caso.
En el dibujo se muestra el ángulo que forma el vector  con el eje + Y. Entonces
con el eje + Y. Entonces
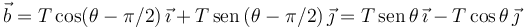
Hemos usado las fórmulas
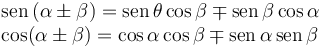
1.3 Caso c
El vector  forma un ángulo θ con el eje − X. Entonces
forma un ángulo θ con el eje − X. Entonces
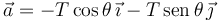
En el dibujo se muestra el ángulo que forma el vector  con el eje + Y. Entonces
con el eje + Y. Entonces
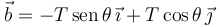
1.4 Caso d
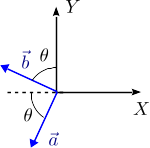
El vector  forma un ángulo θ con el eje − Y. Entonces
forma un ángulo θ con el eje − Y. Entonces
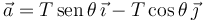
En el dibujo se muestra el ángulo que forma el vector  con el eje − X. Entonces
con el eje − X. Entonces