Primera Convocatoria Ordinaria 2018/19 (MR G.I.C.)

De Laplace

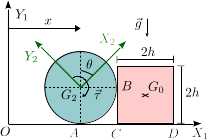
1 Disco empujando una placa

Un disco homogéneo de radio $R$ y masa $m$ (sólido "2") rueda sin deslizar sobre el eje fijo $O X 1$ . El disco empuja una placa homogénea cuadrada (sólido "0") de masa $m$ y lados $2 h$ . La placa desliza sobre el mismo eje fijo. El contacto en el punto $B$ es liso. Sobre el disco actúa un par de fuerzas 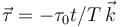$\vec{\tau} = -\tau_0t/T\,\vec{k}$ , siendo $τ 0$ y $T$ constantes con dimensiones de momento de fuerza y tiempo, respectivamente. En el instante inicial el centro del disco estaba sobre el eje $O Y 1$ . El disco y la placa mantienen siempre el contacto. El contacto entre la placa y el suelo es liso. Se cumple $R > h$ .

Escribe la reducción cinemática de los movimientos {21} y {01}.
Dibuja el diagrama de fuerzas y pares que actúan sobre cada sólido.
Aplicando los teoremas fundamentales de la Dinámica Vectorial, encuentra las aceleraciones de los centros de masas de los dos sólidos.
Encuentra el valor de todas las fuerzas que actúan sobre los sólidos. ¿En que instante de tiempo la base de la placa empieza a separarse del suelo?

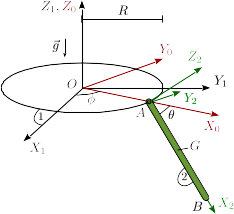
2 Barra colgando de aro fijo

Una barra (sólido "2") homogénea y delgada de longitud $2 R$ y masa $m$ se mueve de modo que su extremo $A$ está obligado a deslizar por un aro fijo de radio $R$ (sólido "1"). Escogemos un sistema de ejes $O X 0 Y 0 Z 0$ de modo que el eje $Z 0$ coincide con el eje $O Z 1$ y el plano $O X 0 Z 0$ contiene en todo momento a la barra. Los ejes solidarios con la barra son tales que el plano $A X 2 Z 2$ coincide siempre con el plano $O X 0 Z 0$ . Entonces se cumple $AY_2\parallel OY_0$ . El eje $A X 0$ forma un ángulo $θ$ con el eje $O X 0$ .

Encuentra la reducción cinemática del movimiento \{21\} en el punto $A$ así como su derivada temporal.
Calcula el momento cinético de la barra en $G$ . Explica como calcularías su momento cinético en $A$ .
Calcula la energía cinética de la barra y su energía potencial.
Se impone el vínculo cinemático 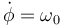$\dot{\phi}=\omega_0$ , siendo $ω 0$ una constante. Escribe la desvinculación de la barra.
Supongamos que la Lagrangiana del sistema tiene la forma 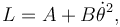$L = A + B\dot{\theta}^2,$ con $A$ y $B$ constantes. El vínculo cinemático del apartado anterior sigue aplicado. El estado de la barra está descrito por $θ(0 -) = π / 2$ y 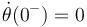$\dot{\theta}(0^-)=0$ . Se aplica una percusión $\vec{\hat{F}} = [\hat{F}_0, \hat{F}_0, 0]_0$ en el punto $B$ . Calcula el estado del sistema justo después de la percusión y el valor de la percusión vincular en $A$ .