Preguntas de test de cinemática del sólido rígido (GIE)

De Laplace

1 Deslizamiento de una barra

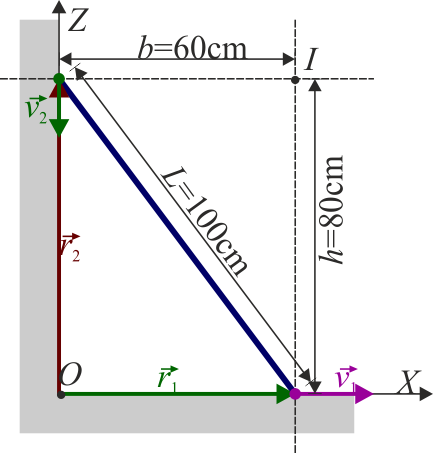
Una barra metálica de 1.00 m de longitud resbala apoyada en el suelo y en una pared vertical. En un momento dado su extremo inferior se encuentra a una distancia de 60\,cm de la esquina y se mueve con velocidad de 12 cm/s alejándose de la esquina

1.1 Pregunta 1

¿Con qué velocidad se mueve el extremo superior de la barra?

A No hay información suficiente para determinarla.
B Está en reposo.
C Desciende con rapidez 9 cm/s.
A Desciende con rapidez 16 cm/s.

Solución

La respuesta correcta es la C.

Existen numerosas maneras de determinar la velocidad del extremo superior.

En primer lugar determinamos la posición de este extremo. Siguiendo la sugerencia del enunciado, consideramos un sistema de ejes centrado en la esquina, con el eje OX en el suelo y el OY en la pared. En este caso, la posición del extremo inferior es

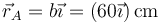
$\vec{r}_A = b\vec{\imath}=(60\vec{\imath})\,\mathrm{cm}$

y la del extremo superior es de la forma

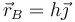
$\vec{r}_B = h\vec{\jmath}$

Hallamos el valor de $h$ por el teorema de Pitágoras

$b^2 +h^2 = L^2\qquad\Rightarrow\qquad h = \sqrt{L^2-b^2} = 80\,\mathrm{cm}$

Las velocidades de estos dos puntos son tangentes a las respectivas superficies de contacto

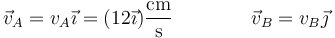
$\vec{v}_A = v_A\vec{\imath} = (12\vec{\imath})\frac{\mathrm{cm}}{\mathrm{s}}\qquad\qquad \vec{v}_B = v_B\vec{\jmath}$

Siendo $v B$ la cantidad que deseamos determinar. De entrada podemos decir que va a resultar una cantidad negativa, pues si el extremo inferior se aleja de la esquina, el otro debe acercarse a ella. Si no, la barra se estaría estirando. Sin embargo, no hace falta suponerlo, sino que resultará solo.

Por la condición de rigidez

La forma más sencilla de hallar la velocidad del extremo superior es aplicando la condición cinemática de rigidez, ya que la barra constituye un sólido rígido. Esto se expresa matemáticamente como las velocidades son equiproyectivas

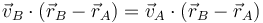
$\vec{v}_B\cdot(\vec{r}_B-\vec{r}_A) = \vec{v}_A\cdot(\vec{r}_B-\vec{r}_A)$

Sustituyendo los datos conocidos

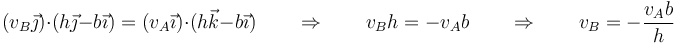
$(v_B\vec{\jmath})\cdot(h\vec{\jmath}-b\vec{\imath}) = (v_A\vec{\imath})\cdot(h\vec{k}-b\vec{\imath})\qquad\Rightarrow\qquad v_Bh = -v_A b\qquad \Rightarrow\qquad v_B = -\frac{v_Ab}{h}$

con el valor numérico, midiendo las distancias en centímetros y el tiempo en segundos,

$(v_B\vec{\jmath})\cdot(80\vec{\jmath}-60\vec{\imath}) = (12\vec{\imath})\cdot(80\vec{\jmath}-60\vec{\imath})\qquad\Rightarrow\qquad 80v_B = -720\qquad \Rightarrow\qquad v_B = -\frac{720}{80}=-9\,\frac{\mathrm{cm}}{\mathrm{s}}$

En forma vectorial

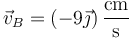
$\vec{v}_B =\left( -9\vec{\jmath}\right)\frac{\mathrm{cm}}{\mathrm{s}}$

Empleando el teorema de Chasles

Podemos hallar la velocidad de B empleando la expresión general del campo de velocidades

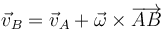
$\vec{v}_B = \vec{v}_A+\vec{\omega}\times\overrightarrow{AB}$

donde, por tratarse de un movimiento plano, tenemos

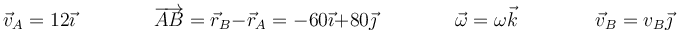
$\vec{v}_A=12\vec{\imath}\qquad \qquad\overrightarrow{AB}=\vec{r}_B-\vec{r}_A=-60\vec{\imath}+80\vec{\jmath}\qquad\qquad \vec{\omega}=\omega\vec{k}\qquad\qquad \vec{v}_B=v_B\vec{\jmath}$

Sustituyendo nos queda

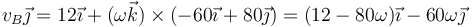
$v_B\vec{\jmath}=12\vec{\imath}+(\omega\vec{k})\times(-60\vec{\imath}+80\vec{\jmath})=(12-80\omega)\vec{\imath}-60\omega\vec{\jmath}$

Igualamos componente a componente

$0 = 12-80\omega\qquad\qquad v_B = -60\omega$

y obtenemos simultáneamente el valor de la velocidad angular de la barra y la del extremo B

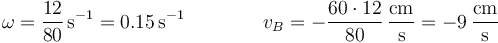
$\omega = \frac{12}{80}\,\mathrm{s}^{-1}=0.15\,\mathrm{s}^{-1}\qquad\qquad v_B = -\frac{60\cdot 12}{80}\,\frac{\mathrm{cm}}{\mathrm{s}} = -9\,\frac{\mathrm{cm}}{\mathrm{s}}$

A partir del CIR

Otra posibilidad para hallar la velocidad del extremo superior es con ayuda del centro instantáneo de rotación. Un sólido rígido en un movimiento plano efectúa en cada instante un movimiento de rotación en torno a su CIR. La rapidez de cada punto es proporcional a la distancia al CIR, por lo que

$\left|\vec{v}_1\right| = |\vec{\omega}|d_1\qquad\qquad \left|\vec{v}_2\right| = |\vec{\omega}|d_2$

Dividiendo una por la otra eliminamos la velocidad angular, que desconocemos

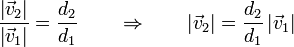
$\frac{\left|\vec{v}_2\right|}{\left|\vec{v}_1\right|} = \frac{d_2}{d_1}\qquad\Rightarrow\qquad \left|\vec{v}_2\right|=\frac{d_2}{d_1}\left|\vec{v}_1\right|$

Tal como se ve en la pregunta siguiente, el CIR se halla, para el instante del enunciado, en

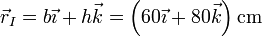
$\vec{r}_I =b\vec{\imath}+h\vec{k}=\left(60\vec{\imath}+80\vec{k}\right)\mathrm{cm}$

y las distancias de lo extremos a este punto valen

$d_1 = h = 80\,\mathrm{cm}\qquad \qquad d_2 = b = 60\,\mathrm{cm}$

lo que nos da la rapidez

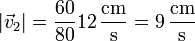
$\left|\vec{v}_2\right| = \frac{60}{80}12\,\frac{\mathrm{cm}}{\mathrm{s}}=9\,\frac{\mathrm{cm}}{\mathrm{s}}$

La dirección de movimiento es tangente a la pared y en sentido hacia abajo, con lo que queda la velocidad

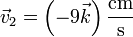
$\vec{v}_2 =\left( -9\vec{k}\right)\frac{\mathrm{cm}}{\mathrm{s}}$

Derivando respecto al tiempo

Una tercera forma consiste en derivar la posición del extremo superior respecto al tiempo. Sabemos que la longitud de la barra es constante en todo momento, por lo que esta posición se puede escribir

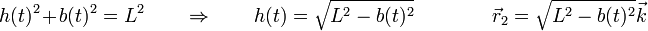
$h(t)^2+b(t)^2 = L^2\qquad\Rightarrow\qquad h(t) = \sqrt{L^2-b(t)^2}\qquad\qquad \vec{r}_2 = \sqrt{L^2-b(t)^2}\vec{k}$

Derivando aquí respecto al tiempo

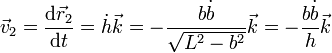
$\vec{v}_2 = \frac{\mathrm{d}\vec{r}_2}{\mathrm{d}t}=\dot{h}\vec{k}=-\frac{b\dot{b}}{\sqrt{L^2-b^2}}\vec{k}=-\frac{b\dot{b}}{h}\vec{k}$

Sustituyendo los datos obtenemos el resultado ya conocido

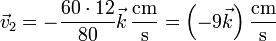
$\vec{v}_2 = -\frac{60\cdot 12}{80}\vec{k}\,\frac{\mathrm{cm}}{\mathrm{s}} =\left( -9\vec{k}\right)\frac{\mathrm{cm}}{\mathrm{s}}$

1.2 Pregunta 2

Considerando un sistema de ejes centrado en la esquina, con el suelo como eje OX y la pared como eje OZ, ¿dónde se encuentra el C.I.R. de la barra en el instante anterior?

A No hay información suficiente para determinarlo.
B En $\vec{r}_I=\vec{0}$ .
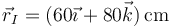C En $\vec{r}_I= (60\vec{\imath}+80\vec{k})\,\mathrm{cm}$ .
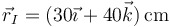A En $\vec{r}_I = (30\vec{\imath}+40\vec{k})\,\mathrm{cm}$ .

Solución

La respuesta correcta es la C.

La forma más sencilla de determinar la posición del centro instantáneo de rotación es mediante un método gráfico. El CIR se encuentra trazando la perpendicular por un punto a la velocidad de dicho punto, para dos puntos diferentes, y localizando la intersección de estas dos rectas.

Para el punto 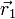$\vec{r}_1$ la perpendicular es la recta vertical que pasa por este punto. La ecuación de esta recta es simplemente

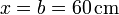
$x = b = 60\,\mathrm{cm}$

Para el punto 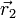$\vec{r}_2$ se trata de la recta horizontal situada a la altura de este extremo

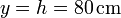
$y = h = 80\,\mathrm{cm}$

El CIR se encuentra en la intersección de estas dos rectas, esto es, es el punto

$x = b = 60\,\mathrm{cm}\qquad\qquad y = h = 80\,\mathrm{cm}$

o, en forma vectorial

$\vec{r}_I = b\vec{\imath}+h\vec{\jmath} = \left(60\vec{\imath}+80\vec{\jmath}\right)\,\mathrm{cm}$

2 Caso particular de movimiento rígido

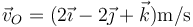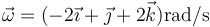En un sólido rígido, la velocidad del origen en un determinado instante es $\vec{v}_O=(2\vec{\imath}-2\vec{\jmath}+\vec{k})\mathrm{m}/\mathrm{s}$ y su velocidad angular $\vec{\omega} = (-2\vec{\imath}+\vec{\jmath}+2\vec{k})\mathrm{rad}/\mathrm{s}$ .

2.1 Pregunta 1

¿Cuánto vale la velocidad instantánea del punto 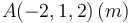$A(-2,1,2)\,(m)$

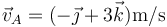
A $\vec{v}_A=(-\vec{\jmath}+3\vec{k})\mathrm{m}/\mathrm{s}$
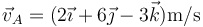
B $\vec{v}_A=(2\vec{\imath}+6\vec{\jmath}-3\vec{k})\mathrm{m}/\mathrm{s}$
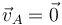
C $\vec{v}_A = \vec{0}$
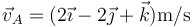
D $\vec{v}_A=(2\vec{\imath}-2\vec{\jmath}+\vec{k})\mathrm{m}/\mathrm{s}$

Solución

La respuesta correcta es la D.

La velocidad del punto A la calculamos empleando el teorema de Chasles

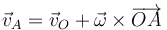
$\vec{v}_A=\vec{v}_O+\vec{\omega}\times\overrightarrow{OA}$

En este caso, en m/s

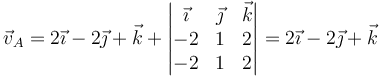
$\vec{v}_A=2\vec{\imath}-2\vec{\jmath}+\vec{k}+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ -2 & 1 & 2 \\ -2 & 1 & 2\end{matrix}\right|=2\vec{\imath}-2\vec{\jmath}+\vec{k}$

La velocidad de A es la misma que la de O por ser la velocidad angular paralela al vector de posición relativo $\overrightarrow{OA}$

2.2 Pregunta 2

¿Qué tipo de movimiento describe el sólido en ese instante?

A Reposo.
B Helicoidal.
C Rotación.
D Traslación.

Solución

La respuesta correcta es la B.

Evidentemente el estado no es de reposo, por haber al menos un punto en movimiento.

Tampo es una traslación, pues la velocidad angular es no nula.

Queda ver si es de rotación o helicoidal. El elemento determinante es si la velocidad angular es perpendicular a las velocidades de los puntos.

Si 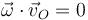$\vec{\omega}\cdot\vec{v}_O = 0$ es un movimiento de rotación.
Si 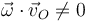$\vec{\omega}\cdot\vec{v}_O \neq 0$ es un movimiento helicoidal.

En nuestro caso

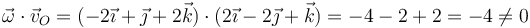
$\vec{\omega}\cdot\vec{v}_O=(-2\vec{\imath}+\vec{\jmath}+2\vec{k})\cdot(2\vec{\imath}-2\vec{\jmath}+\vec{k}) = -4-2+2 = -4 \neq 0$

y por tanto el movimiento es helicoidal.

3 Propiedades de un movimiento

En el movimiento instantáneo de un sólido rígido, un punto A tiene velocidad nula, y un punto B tiene velocidad 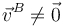$\vec{v}^B\neq \vec{0}$ . ¿Cuál de las siguientes afirmaciones es falsa? (EIRMD: Eje instantáneo de rotación y mínimo deslizamiento)

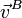A La dirección del EIRMD es perpendicular a $\vec{v}^B$ .
B El EIRMD pasa por A.
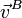C La dirección del EIRMD es paralela a $\vec{v}^B$ .
D El sólido efectúa un movimiento instantáneo de rotación.

Solución

La respuesta correcta es la C.

La D es correcta porque hay un punto con velocidad nula, pero no todos los puntos están en reposo.

El EIR pasa por los puntos de velocidad nula, con lo que la B también es correcta.

La velocidad del punto B cumple

$\vec{v}^B =\vec{v}^A + \vec{\omega}\times\overrightarrow{AC}=\overbrace{\vec{\omega}\times\overrightarrow{AC}}^{\perp \vec{\omega}}$

Por tanto, como la dirección del EIR la da la velocidad angular, la A también es cierta.

Esto deja como falsa la C, ya que la dirección del eje es perpendicular a las velocidades de los puntos, no paralela a ella.

4 Caso de movimiento plano

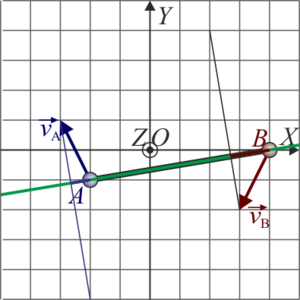
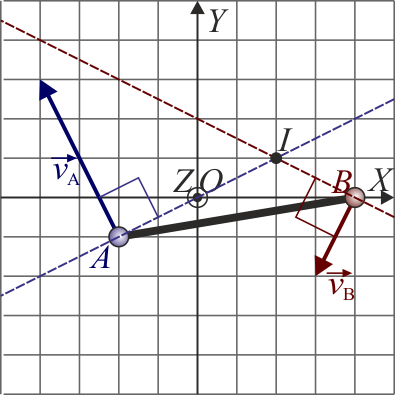
En un movimiento plano, se tiene que la velocidad instantánea de dos puntos A y B es la ilustrada en la figura (para la posición, la cuadrícula representa cm y para la velocidad cm/s)

4.1 Pregunta 1

En dicho instante, ¿cuál es la velocidad del origen de coordenadas O?

A $\vec{0}$
B Estas velocidades son imposibles en el movimiento de un sólido rígido.
C 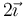$2\vec{\imath}$ (cm/s)
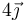D $4\vec{\jmath}$ (cm/s)

Solución

La respuesta correcta es la C.

Podemos hallar la velocidad del punto O:

Aplicando la condición cinemática de rigidez
Mediante la fórmula del campo de velocidades
Gráfica o analíticamente una vez localizado el CIR

Condición de rigidez

La velocidad del origen la podemos escribir como

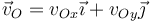
$\vec{v}_O = v_{Ox}\vec{\imath}+v_{Oy}\vec{\jmath}$

Esta velocidad debe cumplir, junto con la del punto A, la condición de rigidez o de equiproyectividad

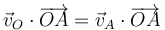
$\vec{v}_O\cdot\overrightarrow{OA}=\vec{v}_A\cdot\overrightarrow{OA}$

donde

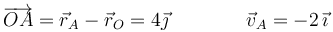
$\overrightarrow{OA}=\vec{r}_A-\vec{r}_O=4\vec{\jmath}\qquad\qquad\vec{v}_A=-2\,\vec{\imath}$

lo que nos da una componente de la velocidad del origen

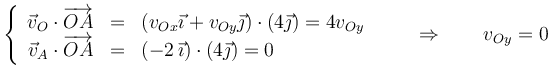
$\left\{\begin{array}{rcl}\vec{v}_O\cdot\overrightarrow{OA}&=&(v_{Ox}\vec{\imath}+v_{Oy}\vec{\jmath})\cdot(4\vec{\jmath})= 4v_{Oy} \\ \vec{v}_A\cdot\overrightarrow{OA}&=&(-2\,\vec{\imath})\cdot(4\vec{\jmath})=0\end{array}\right.\qquad\Rightarrow\qquad v_{Oy}=0$

De manera análoga, tenemos, para el punto B

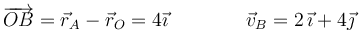
$\overrightarrow{OB}=\vec{r}_A-\vec{r}_O=4\vec{\imath}\qquad\qquad\vec{v}_B=2\,\vec{\imath}+4\vec{\jmath}$

y

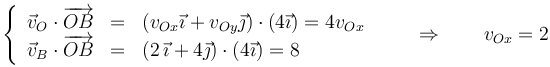
$\left\{\begin{array}{rcl}\vec{v}_O\cdot\overrightarrow{OB}&=&(v_{Ox}\vec{\imath}+v_{Oy}\vec{\jmath})\cdot(4\vec{\imath})= 4v_{Ox} \\ \vec{v}_B\cdot\overrightarrow{OB}&=&(2\,\vec{\imath}+4\vec{\jmath})\cdot(4\vec{\imath})=8\end{array}\right.\qquad\Rightarrow\qquad v_{Ox}=2$

Combinando los dos resultados podemos expresar la velocidad del origen en forma vectorial

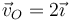
$\vec{v}_O=2\vec{\imath}$

Mediante el campo de velocidades

Calculamos en primer lugar la velocidad angular. Puesto que se trata de un movimiento plano, la velocidad angular es ortogonal a él

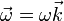
$\vec{\omega}=\omega\vec{k}$

Relacionamos ahora las velocidades de A y B

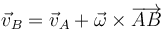
$\vec{v}_B=\vec{v}_A+\vec{\omega}\times\overrightarrow{AB}$

siendo

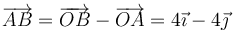
$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=4\vec{\imath}-4\vec{\jmath}$

lo que nos da

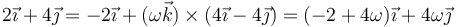
$2\vec{\imath}+4\vec{\jmath} = -2\vec{\imath}+(\omega\vec{k})\times(4\vec{\imath}-4\vec{\jmath}) = (-2+4\omega)\vec{\imath}+4\omega\vec{\jmath}$

Igualando componente a componente

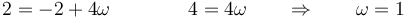
$2 = -2+4\omega\qquad\qquad 4 = 4\omega\qquad\Rightarrow\qquad \omega = 1$

Las dos ecuaciones tienen la misma solución, porque si no no se cumpliría la condición de rigidez. Por tanto

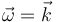
$\vec{\omega}=\vec{k}$

Una vez que tenemos la velocidad angular, hallamos la velocidad del punto O a partir de la de A

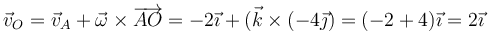
$\vec{v}_O = \vec{v}_A+\vec{\omega}\times\overrightarrow{AO}=-2\vec{\imath}+(\vec{k}\times(-4\vec{\jmath})=(-2+4)\vec{\imath}=2\vec{\imath}$

4.2 Pregunta 2

¿Dónde se encuentra el centro instantáneo de rotación?

A En O.
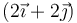B En $(2\vec{\imath}+2\vec{\jmath})$ cm
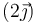C En $(2\vec{\jmath})$ (cm)
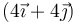D En $(4\vec{\imath}+4\vec{\jmath})$ cm

Solución

La respuesta correcta es la C.

La posición del CIR la podemos determinar tanto analítica como geométricamente.

Determinación analítica

En un movimiento plano, la posición del CIR respecto a un punto A del que conocemos la velocidad es

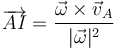
$\overrightarrow{AI}=\frac{\vec{\omega}\times\vec{v}_A}{|\vec{\omega}|^2}$

En nuestro caso, empleando la velocidad angular que ya calculamos

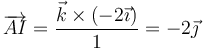
$\overrightarrow{AI}=\frac{\vec{k}\times(-2\vec{\imath})}{1}=-2\vec{\jmath}$

Esta es la posición respecto al punto A. Respecto al origen de coordenadas será

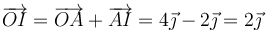
$\overrightarrow{OI}=\overrightarrow{OA}+\overrightarrow{AI}=4\vec{\jmath}-2\vec{\jmath} = 2\vec{\jmath}$

Determinación geométrica

Para hallar geométricamente la posición del CIR observamos que, para todo punto P se cumple

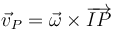
$\vec{v}_P = \vec{\omega}\times\overrightarrow{IP}$

la velocidad de cada punto es ortogonal al vector de posición relativo respecto al CIR.

Trazamos entonces las perpendiculares a las velocidades $\vec{v}_A$ y $\vec{v}_B$ por los puntos respectivos. El CIR se halla en la interesección de estas dos perpendiculares. En este caso este punto tiene por vector de posición

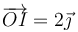
$\overrightarrow{OI}=2\vec{\jmath}$

Velocidad del origen

Una vez que tenemos localizado el CIR y conocemos la velocidad angular, podemos hallar la velocidad de cualquier punto. Para el origen de coordenadas

$\vec{v}_O = \vec{\omega}\times\overrightarrow{IO}=\vec{k}\times(-2\vec{\jmath})=2\vec{\imath}$

5 Posible movimiento de una barra

5.1 Pregunta 1

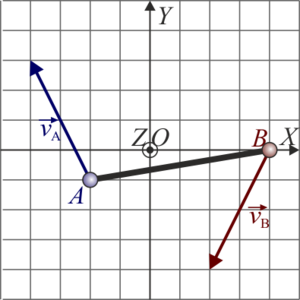
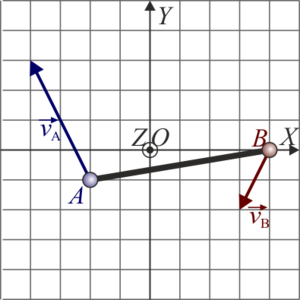
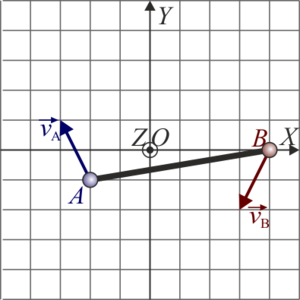
De las siguientes cuatro figuras, solo una representa velocidades posibles de los extremos A y B de una barra rígida que realiza un movimiento plano. ¿Cuál?

A	B


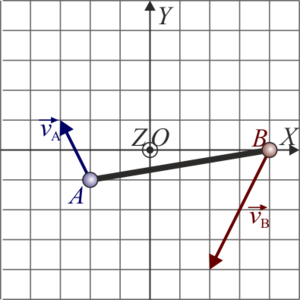
C	D

Solución

La respuesta correcta es la B.

Podemos demostrarlo empleando la condición de rigidez, a partir del campo de velocidades, o localizando previamente el CIR, sobre el cual se pregunta en la siguiente cuestión.

Condición cinemática de rigidez

El campo de velocidades de un sólido rígido debe ser equiproyectivo, es decir

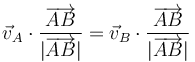
$\vec{v}_A\cdot\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}=\vec{v}_B\cdot\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$

Gráficamente, esto quiete decir que la proyección de las velocidades de las dos partículas sobre la recta que une los dos puntos debe ser igual. Comparando los cuatro casos, vemos que esto sólo ocurre en el caso B.

Diferentes	Iguales


Diferentes	Diferentes

5.2 Pregunta 2

Para la barra anterior, ¿dónde se encuentra su centro instantáneo de rotación, según la cuadrícula de la figura?

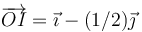
A $\overrightarrow{OI} = \vec{\imath}-(1/2)\vec{\jmath}$
B Está en el infinito.
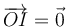
C $\overrightarrow{OI} = \vec{0}$
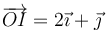
D $\overrightarrow{OI} = 2\vec{\imath}+\vec{\jmath}$

Solución

La respuesta correcta es la D.

Gráficamente, la posición del CIR se halla trazando las perpendiculares a las velocidades de A y B que pasan por A y B respectivamente. La intersección de estas dos perpendiculares es la posición buscada.

En este caso, cualquiera de las cuatro figuras conduce al mismo punto

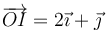
$\overrightarrow{OI} = 2\vec{\imath}+\vec{\jmath}$

Una vez localizado el centro instantáneo de rotación, podemos usarlo para resolver la cuestión anterior. Puesto que la rapidez de un punto de un sólido es proporcional a la distancia al eje

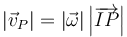
$|\vec{v}_P| = |\vec{\omega}|\left|\overrightarrow{IP}\right|$

y el punto B está más cerca del CIR que el punto A, la solución correcta para las velocidades posibles es aquella que tiene menor rapidez para B que para A, la cual corresponde a la opción B de las respuestas.

5.3 Pregunta 3

¿Cuánto vale, en rad/s, la velocidad angular instantánea de este movimiento, si la cuadrícula representa m en distancias y m/s en velocidades?

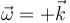
A $\vec{\omega} = +\vec{k}$
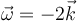
B $\vec{\omega} = -2\vec{k}$
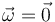
C $\vec{\omega} = \vec{0}$
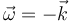
D $\vec{\omega} = -\vec{k}$

Solución

La respuesta correcta es la D.

De acuerdo con la ecuación para la rapidez de los puntos de un sólido tenemos que

$|\vec{v}_B| = |\vec{\omega}|\left|\overrightarrow{IB}\right|\qquad\Rightarrow\qquad |\vec{\omega}| =\frac{ |\vec{v}_B|}{\left|\overrightarrow{IB}\right|}$

En este caso,

$\left|\overrightarrow{IB}\right|=\sqrt{2^2+1^2}\,\mathrm{m}=\sqrt{5}\,\mathrm{m}\qquad\qquad |\vec{v}_B|=\sqrt{1^2+2^2}\,\frac{\mathrm{m}}{\mathrm{s}}=\sqrt{5}\,\frac{\mathrm{m}}{\mathrm{s}}$

y por tanto

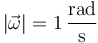
$|\vec{\omega}|=1\,\frac{\mathrm{rad}}{\mathrm{s}}$

El sentido lo da la regla de la mano derecha. La barra está girando en sentido horario y por tanto el vector velocidad angular va hacia adentro del plano, lo que corresponde al eje Z negativo. Por tanto

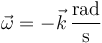
$\vec{\omega}=-\vec{k}\,\frac{\mathrm{rad}}{\mathrm{s}}$

También puede llegarse a este reusltado sin haber determinado previamente el CIR. Tenemos que

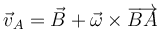
$\vec{v}_A=\vec{B}+\vec{\omega}\times\overrightarrow{BA}$

y por tanto

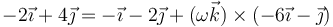
$-2\vec{\imath}+4\vec{\jmath}=-\vec{\imath}-2\vec{\jmath}+(\omega\vec{k})\times(-6\vec{\imath}-\vec{\jmath})$

Calculamos el producto vectorial y separamos en componentes

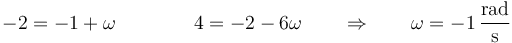
$-2 = -1+\omega\qquad\qquad 4 = -2 -6\omega\qquad\Rightarrow\qquad\omega = -1\,\frac{\mathrm{rad}}{\mathrm{s}}$

y en forma vectorial

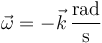
$\vec{\omega}=-\vec{k}\,\frac{\mathrm{rad}}{\mathrm{s}}$

6 Ejemplo de movimiento plano

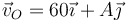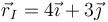Un sólido describe un movimiento plano de forma que el origen de coordenadas tiene una velocidad $\vec{v}_O=60\vec{\imath}+A\vec{\jmath}$ (cm/s), estando el centro instantáneo de rotación en $\vec{r}_I=4\vec{\imath}+3\vec{\jmath}$ (cm).

6.1 Pregunta 1

¿Cuánto vale la constante $A$ ?

A $45$
B $0$ .
C No hay información suficiente para saberlo.
D $- 80$ .

Solución

La respuesta correcta es la D.

El campo de velocidades del sólido debe ser equiproyectivo

$\vec{v}_O\cdot\overrightarrow{IO}=\overbrace{\vec{v}_I}^{=\vec{0}}\cdot\overrightarrow{IO}=0$

por lo que la velocidad del origen debe ser perpendicular a su vector de posición relativo al CIR

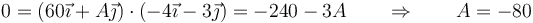
$0=\left(60\vec{\imath}+A\vec{\jmath}\right)\cdot\left(-4\vec{\imath}-3\vec{\jmath}\right)=-240-3A\qquad\Rightarrow\qquad A=-80$

6.2 Pregunta 2

¿Y la velocidad angular del sólido, en rad/s?

A No hay información suficiente para saberlo.
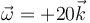
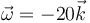
B $\vec{\omega}=+20\vec{k}$
C $\vec{\omega}=-500\vec{k}$
D $\vec{\omega}=-20\vec{k}$

Solución

La respuesta correcta es la B.

La velocidad de cualquier punto es la correspondiente a una rotación en torno al CIR

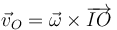
$\vec{v}_O=\vec{\omega}\times\overrightarrow{IO}$

Sustituyendo cada cantidad

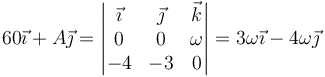
$60\vec{\imath}+A\vec{\jmath}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & \omega \\ -4 & -3 & 0\end{matrix}\right|=3\omega\vec{\imath}-4\omega\vec{\jmath}$

e igualando componente a componente

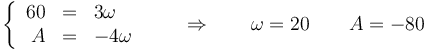
$\left\{\begin{array}{rcl}60 & = & 3\omega \\ A & = & -4\omega\end{array}\right. \qquad\Rightarrow\qquad \omega = 20\qquad A = -80$

En forma vectorial

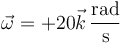
$\vec{\omega}=+20\vec{k}\,\frac{\mathrm{rad}}{\mathrm{s}}$

Nótese que no es preciso determinar previamente el valor de la constante A. El propio cálculo nos da este valor y nos permite responder a la pregunta anterior.

7 Pivotamiento y rodadura

7.1 Pregunta 1

Una bola se encuentra sobre la superficie horizontal $z = 0$ . La velocidad del punto de contacto es nula y la velocidad angular instantánea de la bola es 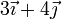$3\vec{\imath}+4\vec{\jmath}$ (rad/s). Podemos decir que…

A Pivota con una velocidad angular de 5 rad/s
B Pivota con una velocidad angular de 4 rad/s y rueda con una de 3 rad/s.
C Rueda con una velocidad angular de 5 rad/s
D Pivota con una velocidad angular de 3 rad/s y rueda con una de 4 rad/s.

Solución

La respuesta correcta es la C.

Este problema, lo que pide es la descomposición de la velocidad angular en rodadura y pivotamiento. $\vec{\omega}$ , como cualquier otro vector se descompone en una parte perpendicular al plano de contacto (y paralela, por tanto, al vector normal a él), que es la velocidad angular de pivotamiento y una tangencial al plano (y perpendicular al vector normal), que es la de rodadura.

En este caso, el vector normal al plano es $\vec{k}$ mientras que, en rad/s

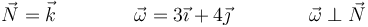
$\vec{N}=\vec{k}\qquad\qquad\vec{\omega}= 3\vec{\imath}+4\vec{\jmath}\qquad\qquad \vec{\omega}\perp\vec{N}$

La velocidad angular no tiene componente normal y por tanto la de pivotamiento es nula

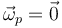
$\vec{\omega}_p=\vec{0}$

y toda la velocidad angular es de rodadura

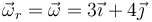
$\vec{\omega}_r=\vec{\omega}=3\vec{\imath}+4\vec{\jmath}$

siendo su módulo

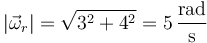
$|\vec{\omega}_r|=\sqrt{3^2+4^2}=5\,\frac{\mathrm{rad}}{\mathrm{s}}$

7.2 Pregunta 2

¿Y si la velocidad angular fuera 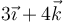$3\vec{\imath}+4\vec{k}$ (rad/s)?

A Pivota con una velocidad angular de 5 rad/s
B Pivota con una velocidad angular de 4 rad/s y rueda con una de 3 rad/s.
C Rueda con una velocidad angular de 5 rad/s
D Pivota con una velocidad angular de 3 rad/s y rueda con una de 4 rad/s.

Solución

La respuesta correcta es la B.

Este caso es similar al anterior con la diferencia de que ahora sí hay componente perpendicular al plano de contacto por lo que, en rad/s

$\vec{N}=\vec{k}\qquad\qquad\vec{\omega}= 3\vec{\imath}+4\vec{k}\qquad\rightarrow\qquad\qquad \vec{\omega}_p=4\vec{k}\qquad\vec{\omega}_r=3\vec{\imath}$

siendo sus módulos

$|\vec{\omega}_p|=4\,\frac{\mathrm{rad}}{\mathrm{s}}\qquad\qquad |\vec{\omega}_r|=3\,\frac{\mathrm{rad}}{\mathrm{s}}$

8 Movimiento de un sólido

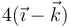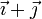Un sólido rígido se mueve de manera que el origen de coordenadas tiene velocidad (en el SI) $4(\vec{\imath}-\vec{k})$ y la velocidad angular del sólido vale $\vec{\imath}+\vec{\jmath}$ .

8.1 Pregunta 1

¿Qué tipo de movimiento describe el sólido?

A Helicoidal
B No hay suficiente información para saberlo.
C Rotación.
D Traslación.

Solución

La respuesta correcta es la A.

La velocidad angular no es nula, por lo que se trata de una rotación o un movimiento helicoidal. Además, la velocidad de un punto y la angular no son vectores perpendiculares

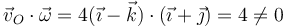
$\vec{v}_O\cdot\vec{\omega}=4(\vec{\imath}-\vec{k})\cdot(\vec{\imath}+\vec{\jmath})=4\neq 0$

Por tanto se trata de un movimiento helicoidal.

8.2 Pregunta 2

¿Cuál de los siguientes es un punto del eje instantáneo de rotación (y mínimo deslizamiento, en su caso)?

A (−1,3,2)
B (2,2,0)
C (1,5,−2)
D (4,0,−2)

Solución

La respuesta correcta es la C.

Los puntos del EIRMD son los que tienen una velocidad lineal paralela a la velocidad angular del sólido

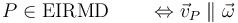
$P\in \textrm{EIRMD}\qquad\Leftrightarrow \vec{v}_P\parallel\vec{\omega}$

La velocidad de cada punto se calcula por el campo de velocidades

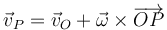
$\vec{v}_P=\vec{v}_O+\vec{\omega}\times \overrightarrow{OP}$

Esta fórmula nos da para el punto A

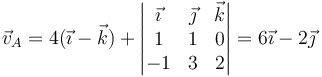
$\vec{v}_A=4(\vec{\imath}-\vec{k})+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1& 1 & 0 \\ -1 & 3 & 2 \end{matrix}\right| = 6\vec{\imath}-2\vec{\jmath}$

Para B

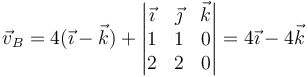
$\vec{v}_B=4(\vec{\imath}-\vec{k})+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1& 1 & 0 \\ 2 & 2 & 0 \end{matrix}\right| = 4\vec{\imath}-4\vec{k}$

Para C

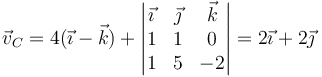
$\vec{v}_C=4(\vec{\imath}-\vec{k})+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1& 1 & 0 \\ 1 & 5 & -2 \end{matrix}\right| = 2\vec{\imath}+2\vec{\jmath}$

y para D

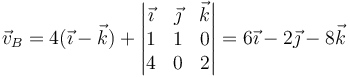
$\vec{v}_B=4(\vec{\imath}-\vec{k})+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1& 1 & 0 \\ 4 & 0 & 2 \end{matrix}\right| = 6\vec{\imath}-2\vec{\jmath} -8\vec{k}$

De estos cuatro vectores, solo es paralelo a $\vec{\omega}$ el del punto C, que por tanto se halla en el EIRMD.

Otra forma de verlo es considerar un punto genérico

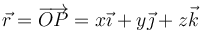
$\vec{r}=\overrightarrow{OP}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}$

para el cual la velocidad es

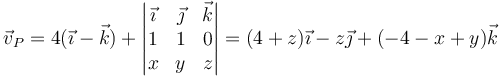
$\vec{v}_P=4(\vec{\imath}-\vec{k})+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 1& 1 & 0 \\ x & y & z \end{matrix}\right| = (4+z)\vec{\imath}-z\vec{\jmath}+ (-4-x+y)\vec{k}$

Este vector es paralelo a

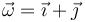
$\vec{\omega}=\vec{\imath}+\vec{\jmath}$

si

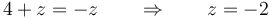
$4+z=-z \qquad \Rightarrow\qquad z=-2$

y

$-4-x+y = 0 \qquad\Rightarrow\qquad y = 4+x$

por lo cual, de los cuatro puntos solo el C(1,5,−2) pertenece al EIRMD.

Preguntas de test de cinemática del sólido rígido (GIE)

De Laplace

Contenido

1 Deslizamiento de una barra

1.1 Pregunta 1

1.2 Pregunta 2

2 Caso particular de movimiento rígido

2.1 Pregunta 1

2.2 Pregunta 2

3 Propiedades de un movimiento

4 Caso de movimiento plano

4.1 Pregunta 1

4.2 Pregunta 2

5 Posible movimiento de una barra

5.1 Pregunta 1

5.2 Pregunta 2

5.3 Pregunta 3

6 Ejemplo de movimiento plano

6.1 Pregunta 1

6.2 Pregunta 2

7 Pivotamiento y rodadura

7.1 Pregunta 1

7.2 Pregunta 2

8 Movimiento de un sólido

8.1 Pregunta 1

8.2 Pregunta 2

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES