Entrar Página Discusión Historial Go to the site toolbox

Potencial y energía electrostática (GIOI)

De Laplace

Contenido

1 Trabajo y energía potencial

1.1 Trabajo para mover una carga eléctrica

Supongamos que tenemos una carga positiva “1” en una posición fija del espacio, y deseamos acercar otra carga positiva “2” desde un punto A a un punto B más próximo a la primera. Para hacerlo debemos vencer la repulsión eléctrica ejercida por la primera, aplicando una fuerza externa.

Por tanto, para acercar la carga debemos realizar un trabajo

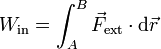
W_\mathrm{in}=\int_A^B \vec{F}_\mathrm{ext}\cdot\mathrm{d}\vec{r}

De acuerdo con el primer principio de la termodinámica, este trabajo realizado sobre el sistema, o bien se almacena como un aumento de la energía total, o bien sale en forma de calor (o una parte de cada cosa)

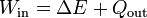
W_\mathrm{in}=\Delta E + Q_\mathrm{out}\,

Si el proceso es cuasiestático, moviendo la carga 2 de forma extremadamente lenta, este trabajo se almacena en forma de energía potencial (que es parte de la energía total). Podemos verlo con el siguiente experimento mental: si una vez en la posición final B, sujetamos la carga 2 con una chincheta y esperamos un cierto tiempo, tras el cual la liberamos, la carga 2 sale disparada por la repulsión de la 1. Al hacerlo, gana energía cinética, ¿de dónde sale esta energía? No vale decir que se la da la carga 1 por su fuerza eléctrica, pues la energía se conserva y la carga 1 no pierde nada. Concluimos entonces, que la carga 2 ya tenía esa energía “guardada” en forma de energía potencial por el hecho de estar en presencia de la 1.

Usando la analogía mecánica, sería equivalente a comprimir un muelle (invisible), realizando para ello una fuerza en contra de la elástica. Se sujeta el muelle con un tope y pasado un tiempo, se retira éste. El muelle se estira empujando la masa, que se acelera. Podemos decir que la energía cinética que gana procede de la energía potencial elástica que tenía por estar el muelle comprimido.

Este razonamiento es generalizable al movimiento de una carga en un campo eléctrico cualquiera (no necesariamente el de una sola carga, sino el de una distribución). Al mover la carga debemos realizar un trabajo, que queda guardado como energía potencial electrostática.

1.2 Energía potencial electrostática

Para hallar una expresión para la energía potencial suponemos que movemos una carga el seno de un campo eléctrico de manera cuasiestática. Para ello debemos ejercer una fuerza que supere a la eléctrica, pero solo ligeramente (pues la partícula no se llega a acelerar)

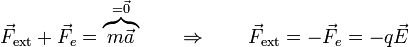
\vec{F}_\mathrm{ext}+\vec{F}_e = \overbrace{m\vec{a}}^{=\vec{0}}\qquad\Rightarrow\qquad \vec{F}_\mathrm{ext}=-\vec{F}_e = -q\vec{E}

por lo que el trabajo realizado es

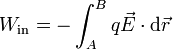
W_\mathrm{in} = -\int_A^B q\vec{E}\cdot\mathrm{d}\vec{r}

En principio, esta integral depende del camino que se recorra. Sin embargo, para el caso del campo de una carga puntual es fácil demostrar (como veremos) que solo depende de la distancia inicial y final a la carga que crea el campo. Puesto que todo campo electrostático es suma de campos de cargas puntuales, se llega a que para cualquier campo electrostático, la integral es independiente del camino y equivale al incremento de una energía potencial

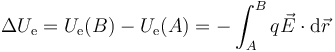
\Delta U_\mathrm{e} = U_{\mathrm{e}}(B)-U_{\mathrm{e}}(A)=-\int_A^B q\vec{E}\cdot\mathrm{d}\vec{r}

Definimos entonces la energía potencial de una carga puntual en un campo eléctrico como la integral

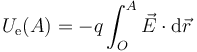
U_{\mathrm{e}}(A) = -q\int_O^A \vec{E}\cdot\mathrm{d}\vec{r}

siendo O un punto de referencia al cual se le asigna energía potencial 0. Para campos debidos a distribuciones localizadas de carga se suele tomar el infinito como referencia. En problemas concretos se puede elegir otro punto que sea más conveniente. Es importante, a la hora de resolver un problema que, una vez elegido el punto de referencia, este no se cambie.

La energía potencial electrostática puede ser tanto positiva como negativa, y su incremento puede tener también los dos signos.

  • Si acercamos una carga positiva a otra carga positiva (o en general a un campo que la repele) debemos hacer un trabajo positivo y la energía potencial aumenta.
  • Si en el mismo campo anterior la carga que acercamos es negativa, resulta un trabajo negativo y una disminución de la energía potencial. ¿Cómo se explica esto físicamente? En este caso, el campo atrae a la carga, por lo que la fuerza que debemos hacer es para retenerla e impedir que se acelere. Esto nos permite extraer energía de la carga (que disipamos por rozamiento, o guardamos en algún tipo de acumulador, como puede ser un resorte o un tubo de aire comprimido).
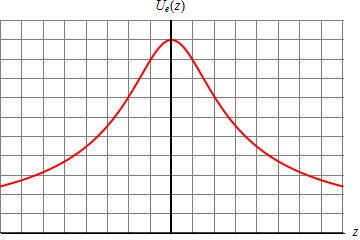
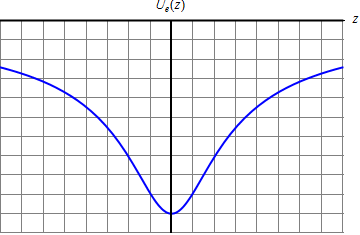
Archivo:energia-potencial-anillo-p.png        Archivo:energia-potencial-anillo-n.png

Las gráficas representan la energía potencial de una carga en el campo eléctrico de un anillo. La curva en forma de montaña corresponde a que la carga y el anillo tengan el mismo signo, y la curva en forma de valle a que tengan signo opuesto.

Una vez establecida la curva de energía potencial, puede aplicarse todo el análisis visto en Mecánica, de curvas de potencial estudiando los casos de equilibrio estable o inestable, los puntos de retorno, movimiento oscilatorio, etc.

2 Potencial eléctrico

2.1 Definición

La energía potencial electrostática depende no solo del campo eléctrico, sino también del valor de la carga que situamos en él. Para un mismo campo eléctrico, una carga q almacena una cierta energía, y una 2q almacenará el doble, y una − q tendrá una energía del signo opuesto. Nos preguntamos entonces como podemos definir una cantidad similar a la energía potencial, pero que dependa solo del campo existente, y no de la carga que situamos.

Puesto que la energía potencial electrostática de una carga es proporcional al valor de ésta, podemos definir el potencial eléctrico en el punto A, de manera análoga a como se define el campo eléctrico,como

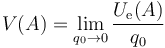
V(A) = \lim_{q_0\to 0}\frac{U_{\mathrm{e}}(A)}{q_0}

es decir, el potencial eléctrico representa la energía potencial por unidad de carga. Se mide en J/C y a esta unidad se la denomina voltio (V).

Sustituyendo la expresión de la energía potencial queda la expresión alternativa, y más frecuente,

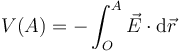
V(A) = -\int_O^A \vec{E}\cdot\mathrm{d}\vec{r}

siendo 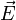\vec{E} el campo eléctrico existente (sin incluir el de la carga que movemos). El punto O es el origen de potencial, para el cual se considera que el potencial eléctrico es nulo. El origen de potencial se denomina normalmente “tierra” (porque normalmente el suelo funciona como referencia de potencial) y decir que un conductor “está a tierra” equivale a decir que su potencial es cero (también se dice “está a masa”).

De esta relación entre campo y potencial se deduce que el campo eléctrico también se puede medir en V/m (que de hecho es su unidad más habitual) siendo 1 V/m = 1 N/C.

El potencial eléctrico respecto a la energía potencial electrostática viene a ser análogo a la altura respecto a la gravitatoria. La energía potencial gravitatoria depende de la masa que subamos, pero la altura es independiente de ella. El origen de potencial sería el nivel que tomemos como referencia (el suelo, por ejemplo). En esta analogía, cuando se ve que la corriente eléctrica fluye de más a menos potencial, sería análogo a decir que el agua por una tubería va “cuesta abajo” y una fuente de tensión que sube el potencial de una carga equivaldría a una bomba que eleva el agua hasta una cierta altura.

Al potencial eléctrico se lo denomina también voltaje y tensión.

El potencial eléctrico es un campo escalar que asigna un número (con un signo y una unidad) a cada punto del espacio.

La ventaja de trabajar con el potencial en lugar de con el campo es que este último es una magnitud vectorial y requiere manejar tres componentes, frente a una del potencial. Conocido el potencial eléctrico puede hallarse el campo eléctrico mediante el gradiente

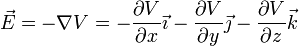
\vec{E}=-\nabla V = -\frac{\partial V}{\partial x}\vec{\imath}-\frac{\partial V}{\partial y}\vec{\jmath}-\frac{\partial V}{\partial z}\vec{k}

El signo negativo que aparece tanto en la definición integral como en el gradiente implica que:

El campo electrostático va siempre en el sentido de mayor a menor potencial eléctrico

2.2 Superficies equipotenciales

Una de las formas de visualizar el potencial eléctrico es mediante las superficies equipotenciales, que son aquellas formadas por los puntos que tienen el mismo potencial. Vienen a ser equivalentes a las curvas de nivel en un mapa topográfico o las isobaras en un mapa del tiempo (pero en 3 dimensiones). Puesto que el potencial eléctrico tiene un solo valor en cada punto del espacio, se deduce que las superficies equipotenciales no pueden cortarse entre sí.

De la relación entre el potencial y el campo eléctrico se demuestra que éste es siempre ortogonal a las superficies equipotenciales.

2.3 Diferencia de potencial

En muchas situaciones no estamos interesados tanto en el valor del potencial, sino en cuanto cambia de un punto a otro. Esto se mide con la diferencia de potencial (d.d.p.)

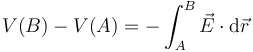
V(B) - V(A) = -\int_A^B \vec{E}\cdot\mathrm{d}\vec{r}

o, intercambiando los subíndices

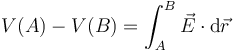
V(A) - V(B) = \int_A^B \vec{E}\cdot\mathrm{d}\vec{r}

Esta integral es independiente del camino que se elija para ir de A a B (aunque alguno hay que elegir). Se denomina también caída de tensión.

La diferencia de potencial se mide en voltios, como el propio potencial eléctrico.

La diferencia de potencial se relaciona directamente con el trabajo para mover una carga puntual, ya que

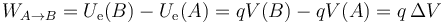
W_{A\to B}= U_{\mathrm{e}}(B)-U_{\mathrm{e}}(A) = qV(B) - q V(A) = q\,\Delta V\,

es decir, el trabajo para mover una carga entre dos puntos en un campo externo es igual al producto de la carga por la diferencia de potencial entre los puntos. Si la carga es positiva, es necesario realizar un trabajo positivo para subir su potencial (su “altura”) y negativo para bajarlo. Al contrario, si la carga es negativa.

2.4 Potencial de una carga puntual

A partir del campo eléctrico de una carga puntual situada en el origen de coordenadas

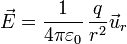
\vec{E}=\frac{1}{4\pi\varepsilon_0}\,\frac{q}{r^2}\vec{u}_r

Podemos hallar el potencial eléctrico considerando el origen de potencial en el infinito. Integrando a lo largo de un camino rectilíneo radial

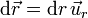
\mathrm{d}\vec{r}=\mathrm{d}r\,\vec{u}_r

y queda, para un punto situada a una distancia r de la carga

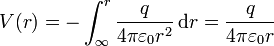
V(r) = -\int_\infty^r \frac{q}{4\pi\varepsilon_0 r^2}\,\mathrm{d}r = \frac{q}{4\pi\varepsilon_0 r}

Las superficies equipotenciales en este caso son esferas concéntricas, que por supuesto son ortogonales al campo eléctrico, que es puramente radial.

Si lo que se conoce es el potencial, el campo eléctrico puede determinarse calculando su gradiente

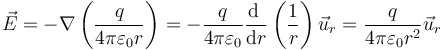
\vec{E}=-\nabla\left(\frac{q}{4\pi\varepsilon_0 r}\right)= -\frac{q}{4\pi\varepsilon_0}\frac{\mathrm{d}\ }{\mathrm{d}r}\left(\frac{1}{r}\right)\vec{u}_r=\frac{q}{4\pi\varepsilon_0 r^2}\vec{u}_r

Más en general, para una carga situada en un punto arbitrario, el potencial será la cantidad escalar

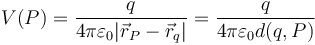
V(P) = \frac{q}{4\pi\varepsilon_0|\vec{r}_P-\vec{r}_q|}=\frac{q}{4\pi\varepsilon_0 d(q,P)}

donde 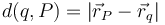d(q,P) = |\vec{r}_P-\vec{r}_q| es la distancia entre la carga y el punto donde queremos hallar el potencial.

Del mismo modo, la diferencia de potencial depende solamente de las distancias inicial y final a la carga

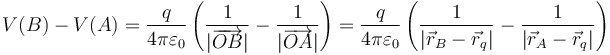
V(B)-V(A) = \frac{q}{4\pi\varepsilon_0}\left(\frac{1}{|\overrightarrow{OB}|}-\frac{1}{|\overrightarrow{OA}|}\right)= \frac{q}{4\pi\varepsilon_0}\left(\frac{1}{|\vec{r}_B-\vec{r}_q|}-\frac{1}{|\vec{r}_A-\vec{r}_q|}\right)

2.5 Existencia del potencial electrostático

La existencia de este potencial eléctrico permite establecer el potencial para cualquier distribución electrostática de cargas, ya que, por el principio de superposición, el campo debido a una distribución se puede escribir como suma de los campos de cargas puntuales

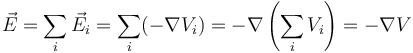
\vec{E}=\sum_i \vec{E}_i=\sum_i (-\nabla V_i)=-\nabla\left(\sum_i V_i\right)=-\nabla V

Por tanto, el potencial debido a una distribución de cargas puntuales, tomando para todas ellas el origen de potencial en el infinito será

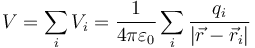
V=\sum_i V_i=\frac{1}{4\pi\varepsilon_0}\sum_i \frac{q_i}{|\vec{r}-\vec{r}_i|}

2.6 Potencial debido a una distribución de cargas

En el caso de una distribución continua el potencial puede calcularse por integración directa de los potenciales debidos a los elementos de carga

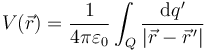
V(\vec{r})=\frac{1}{4\pi\varepsilon_0}\int_Q\frac{\mathrm{d}q'}{\left|\vec{r}-\vec{r}^{\,\prime}\right|}

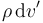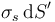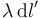siendo el diferencial de carga igual a \rho\,\mathrm{d}v', \sigma_s\,\mathrm{d}S' o \lambda\,\mathrm{d}l' según el tipo de distribución de que se trate. La integral se extiende a todos los puntos del espacio en que hay densidad de carga aunque puede extenderse sin problemas a todo el espacio sin más que hacer nula la densidad de carga en los puntos en que no hay cargas presentes.

Es importante la distinción entre los dos vectores de posición:

  • \vec{r} (sin prima) es la posición del punto donde queremos hallar el potencial eléctrico.
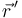  • \vec{r}^{\,\prime} (con prima) es la posición del punto donde se encuentra un elemento de carga.

La integral se hace sobre las variables con prima, ya que sumamos para todos los elementos de carga. La variable sin prima es un punto concreto del espacio y como tal funciona como una constante respecto a la integral. El resultado es una función de \vec{r}.

Por tanto, disponemos de dos formas alternativas para determinar el potencial eléctrico:

  • Integrando el campo eléctrico siguiendo un cierto camino desde el origen de potencial.
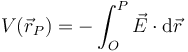
V(\vec{r}_P)=-\int_O^P \vec{E}\cdot\mathrm{d}\vec{r}
  • Por integración directa a partir de la densidad de carga.
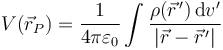
V(\vec{r}_P)=\frac{1}{4\pi\varepsilon_0}\int \frac{\rho(\vec{r}^{\,\prime})\,\mathrm{d}v'}{\left|\vec{r}-\vec{r}^{\,\prime}\right|}

Existe un tercer camino, que de hecho es más usado, consistente en resolver la ecuación diferencial de Poisson, cuyo nivel se escapa a este curso.

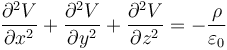
\frac{\partial^2V}{\partial x^2}+\frac{\partial^2V}{\partial y^2}+\frac{\partial^2V}{\partial z^2}=-\frac{\rho}{\varepsilon_0}

Si lo que se desea es determinar el campo eléctrico a partir del potencial, el camino a emplear es el segundo.

Así, por ejemplo, el potencial en el centro de una esfera cargada uniformemente en su superficie puede hallarse a partir del campo o por integración directa. Sin embargo, no siempre los dos métodos son sencillos de aplicar. La integración directa implica habitualmente cálculos tan complicados que requieren el uso de ordenadores. La integración a partir del campo requiere que conozcamos previamente éste, lo cual no siempre es posible.

2.6.1 Potencial de dos cargas puntuales

Puesto que el campo eléctrico de un conjunto de cargas es la suma de los campos individuales, su integral, el potencial eléctrico, también lo será. Eso sí, hay que tener cuidado con tomar el mismo origen de potencial para todos los potenciales individuales.

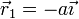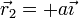Así, si tenemos dos cargas q1 y q2 situadas en dos puntos situados en \vec{r}_1=-a\vec{\imath} y \vec{r}_2=+a\vec{\imath}, el potencial eléctrico debido a ellas es

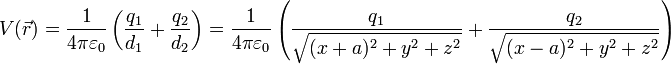
V(\vec{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q_1}{d_1}+\frac{q_2}{d_2}\right) = \frac{1}{4\pi\varepsilon_0}\left(\frac{q_1}{\sqrt{(x+a)^2+y^2+z^2}}+\frac{q_2}{\sqrt{(x-a)^2+y^2+z^2}}\right)

En el caso de dos cargas positivas iguales resulta un potencial positivo en todos los puntos del espacio. En este caso, el campo eléctrico es nulo en el punto medio entre las dos cargas, mientras que el potencial es distinto de 0.

        

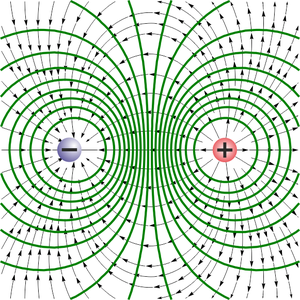
Si lo que tenemos es un dipolo, con cargas de la misma magnitud, pero signo opuesto, el potencial puede tener los dos signos. En el punto medio entre las dos cargas el campo eléctrico no es nulo, pero el potencial sí. De hecho, en todo el plano equidistante entre las dos cargas el potencial se anula, ya que esos puntos equidistan de las dos cargas

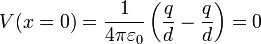
V(x=0)= \frac{1}{4\pi\varepsilon_0}\left(\frac{q}{d}-\frac{q}{d}\right)=0

3 Energía electrostática de un sistema

En el cálculo anterior de la energía potencial eléctrica dijimos que para acercar una carga a otra del mismo signo era preciso realizar un trabajo y que este trabajo quedaba almacenado como energía potencial, lo que se ponía de manifiesto en que si, pasado un tiempo, se liberaba la carga, salía disparada, transformando su energía potencial en cinética.

Sin embargo, existe una visión más general de este proceso. Consideremos que tenemos las dos cargas. Traer la primera no supone trabajo alguno, pues no hay que vencer fuerza alguna. La fijamos en su posición final. Ahora acercamos la segunda carga, realizando el trabajo indicado

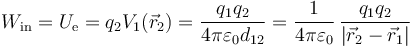
W_\mathrm{in}=U_\mathrm{e}=q_2 V_1(\vec{r}_2) = \frac{q_1q_2}{4\pi\varepsilon_0 d_{12}}=\frac{1}{4\pi\varepsilon_0}\,\frac{q_1q_2}{|\vec{r}_2-\vec{r}_1|}

Fijamos la segunda carga en la posición final. Ahora, en lugar de liberar la segunda carga, liberamos la primera. ¿Qué ocurre entonces? Que esta sale disparada, repelida por q2. ¿De dónde saca la energía si dijimos que el traer la primera no requiere trabajo? La respuesta es que el trabajo que hacemos al acercar la segunda no se queda como energía solo de esta. Tampoco es que se reparta mitad y mitad entre las dos, ya que una vez que se ha alejado la primera, si ahora soltamos la segunda, no se mueve (ya no hay nadie que la repela), por lo que toda la energía se la ha llevado q1. Interpretamos entonces que le energía no está en una carga o en otra sino como energía almacenada en el sistema, a disposición de cada una de las cargas. Asimismo, es indiferente a qué carga llamemos “la primera” o “la segunda”. Una vez que están reunidas, el orden de llegada queda olvidado.

La razón es que la energía eléctrica de un sistema es una función de estado. Solo depende de la posición de las cargas en una configuración dada. Nos interesa entonces una expresión para la energía que sea simétrica sin distinción de cual ponemos antes y cuál más tarde. Para ello, observamos que

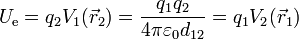
U_\mathrm{e}=q_2 V_1(\vec{r}_2) = \frac{q_1q_2}{4\pi\varepsilon_0 d_{12}}=q_1V_2(\vec{r}_1)

es decir que la energía potencial de la segunda en el campo de la primera es igual a la de la primera en el campo de la segunda. Podemos escribir entonces como forma simétrica la media de ambas

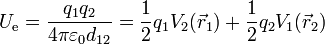
U_\mathrm{e}= \frac{q_1q_2}{4\pi\varepsilon_0 d_{12}} = \frac{1}{2}q_1V_2(\vec{r}_1)+\frac{1}{2}q_2V_1(\vec{r}_2)

Esta expresión se generaliza de forma inmediata a cualquier conjunto de cargas puntuales. La energía almacenada por un sistema es

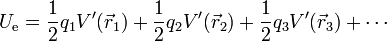
U_\mathrm{e}=\frac{1}{2}q_1V'(\vec{r}_1) + \frac{1}{2}q_2V'(\vec{r}_2) + \frac{1}{2}q_3V'(\vec{r}_3)+\cdots

donde 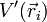V'(\vec{r}_i) es el potencial creado por el resto de cargas del universo en la posición de la carga i (es decir, el potencial total menos el debido a la propia carga qi). Sustituyendo el potencial de cada una de las cargas queda el doble sumatorio

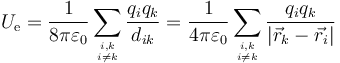
U_\mathrm{e}=\frac{1}{8\pi\varepsilon_0}\sum_{{i,k}\atop {i\neq k}}\frac{q_iq_k}{d_{ik}}=\frac{1}{4\pi\varepsilon_0}\sum_{{i,k}\atop {i\neq k}}\frac{q_iq_k}{|\vec{r}_k-\vec{r}_i|}

En el caso de que tengamos una distribución de carga de volumen o superficial (pero no una lineal), la expresión anterior se generaliza a

U_\mathrm{e}=\frac{1}{2}\int \rho V(\vec{r})\,\mathrm{d}v\qquad\qquad U_\mathrm{e}=\frac{1}{2}\int \sigma_s V(\vec{r})\,\mathrm{d}S

En estas expresiones no hace falta restar la contribución del propio elemento de carga, por ser ésta despreciable.

Si tenemos dos o más distribuciones simultáneamente, la energía será la suma de las integrales (y sumatorios) correspondientes

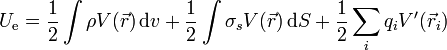
U_\mathrm{e}= \frac{1}{2}\int \rho V(\vec{r})\,\mathrm{d}v+\frac{1}{2}\int \sigma_s V(\vec{r})\,\mathrm{d}S+\frac{1}{2}\sum_iq_iV'(\vec{r}_i)

Una propiedad importante de la energía electrostática de un sistema es que NO verifica el principio de superposición. La energía de dos distribuciones superpuestas no es igual a la suma de las energías que tendrían por separado.

Por ejemplo, si tenemos una nube esférica de radio R con una carga +Q, se obtiene, integrando, una energía

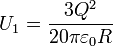
U_1 = \frac{3Q^2}{20\pi\varepsilon_0 R}

esta energía es independiente del signo de la carga, es decir que una nube de carga positiva y una de carga negativa tienen la misma energía (positiva en ambos casos, pues hay repulsión en los dos casos). Si ahora superponemos una nube de carga negativa -Q superpuesta a la nube positiva, el resultado no es el doble de energía, sino que nos quedamos sin nada, ya que los campos se cancelan mutuamente, el potencial total es nulo y la energía también vale cero.

3.1 Energía en función del campo

Puede demostrarse que la energía de una distribución volumétrica y/o superficial de cargas puede calcularse mediante la expresión alternativa

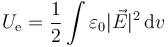
U_\mathrm{e}=\frac{1}{2}\int \varepsilon_0 |\vec{E}|^2\,\mathrm{d}v

donde la integral no se extiende solo a donde haya carga, sino a todo el espacio.

Esta expresión alternativa se puede interpretar de una manera diferente a la expresión anterior. En aquella, se consideraba que la energía la almacenaban conjuntamente las cargas, por estar en presencia de otras. En esta versión la energía la almacena el propio campo eléctrico por el hecho de existir.

Usando la analogía mecánica del muelle, la primera expresión equivale a decir que la energía la tienen las masas situadas en el extremo del muelle y es una energía potencial elástica (eléctrica en este caso); la segunda versión equivale a que la energía la almacena el muelle, por estar comprimido. Vemos más intuitiva la segunda interpretación en el caso del muelle, con el campo eléctrico es lo mismo, solo que el “muelle” es invisible e inmaterial.

La expresión en función del campo puede escribirse en la forma

U_\mathrm{e}=\int u_\mathrm{e}\,\mathrm{d}v\qquad\qquad u_e =\frac{1}{2}\varepsilon_0|\vec{E}|^2

donde ue es la densidad de energía eléctrica (medida en J/m³). Veríamos entonces la energía eléctrica como repartida por todo el espacio, estando más concentrada donde el campo es más intenso.

En electrostática, las dos expresiones para la energía eléctrica de una distribución son equivalentes. Sin embargo, en situaciones variables en el tiempo, solo es válida la segunda (ya que para campos variables en el tiempo no se puede definir el potencial eléctrico). Es más, a la hora de estudiar el campo gravitatorio en relatividad, se comprueba que la simple existencia de un campo eléctrico produce campos gravitatorios, por tanto, la visión correcta es admitir que el campo es un ente capaz de almacenar energía, y no son las cargas las que la tienen.

Obtenido de "http://tesla.us.es/wiki/index.php/Potencial_y_energ%C3%ADa_electrost%C3%A1tica_(GIOI)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 17:02, 26 feb 2020. - Esta página ha sido visitada 1.288 veces. - Aviso legal - Acerca de Laplace