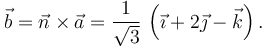De Laplace

1 Enunciado

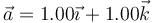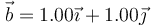Se tienen los vectores $\vec{a}=1.00\vec{\imath} + 1.00\vec{k}$ y $\vec{b} = 1.00\vec{\imath} + 1.00\vec{\jmath}$ . Encuentra la ecuación del plano que es paralelo a los dos vectores y contiene al origen de coordenadas. Encuentra el vector que resulta de rotar $π / 2$ el vector $\vec{a}$ en este plano.

2 Solución

Construimos un vector perpendicular al plano haciendo el producto vectorial de los dos vectores dados

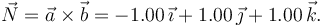
$\vec{N} = \vec{a}\times\vec{b} = -1.00\,\vec{\imath} + 1.00\,\vec{\jmath} + 1.00\,\vec{k}.$

La ecuación de un plano perpendicular a $\vec{N}$ es

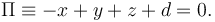
$\Pi \equiv -x + y + z + d=0.$

Hemos usado que los coeficientes de $x$ , $y$ , $z$ son las componentes del vector normal al plano. Como debe pasar por el origen, se tiene

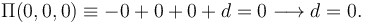
$\Pi(0,0,0) \equiv -0 + 0 + 0 + d=0 \longrightarrow d =0.$

La ecuación final del plano es

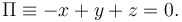
$\Pi \equiv -x + y + z =0.$

Para rotar $π / 2$ radianes el vector $\vec{a}$ , que está contenido en el plano, podemos multiplicarlo vectorialmente por un vector unitario normal al plano. Este vector se calcula así

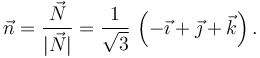
$\vec{n} = \dfrac{\vec{N}}{|\vec{N}|} = \dfrac{1}{\sqrt{3}}\,\left( -\vec{\imath} + \vec{\jmath} + \vec{k}\right).$