De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una varilla delgada (sólido "2") de masa $m$ y longitud $2 b$ está articulada en un pasador (punto $A$ ) que desliza sobre el eje fijo $O Y 1$ .

Calcula la reducción cinemática en el punto $A$ del movimiento {21}.
Calcula la energía cinética de la varilla y su energía potencial.
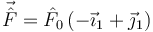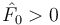Cuando la varilla se encuentra en reposo y con $x = 0$ y $θ = 0$ , se aplica en el punto $C$ una percusión $\vec{\hat{F}} = \hat{F}_0\,(-\vec{\imath}_1 + \vec{\jmath}_1)$ , con $\hat{F}_0>0$ . Determina el movimiento de la varilla justo después de la percusión así como el valor de la percusión vincular en $A$ .
Discute el movimiento del punto $A$ en función del valor de $s$ . ¿Donde está el centro de percusión de $A$ ?

2 Solución

2.1 Reducción cinemática

La reducción cinemática en el punto $A$ es

$\vec{\omega}_{21} = \dot{\theta}\,\vec{k}_1, \qquad \vec{v}^{\,A}_{21} = \dot{x}\,\vec{\jmath}_1$

El sólido tiene dos grados de libertad: ${x,θ}$ .

2.2 Energía cinética y potencial

Calculamos la energía cinética pasando por el centro de masas del sólido

$T = T T + T R$

La energía cinética de traslación es

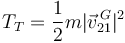
$T_{T} = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2$

La velocidad del centro de masas es

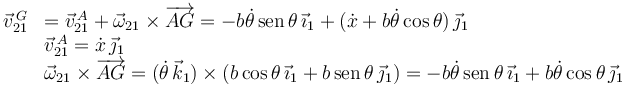
$\begin{array}{ll} \vec{v}^{\,G}_{21}& = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AG} = -b\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + (\dot{x} + b\dot{\theta}\cos\theta)\,\vec{\jmath}_1 \\ & \vec{v}^{\,A}_{21} = \dot{x}\,\vec{\jmath}_1\\ & \vec{\omega}_{21}\times\overrightarrow{AG} = (\dot{\theta}\,\vec{k}_1)\times (b\cos\theta\,\vec{\imath}_1 + b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1) = -b\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + b\dot{\theta}\cos\theta\,\vec{\jmath}_1 \end{array}$

Por tanto, la energía cinética de traslación es

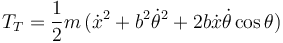
$T_T = \dfrac{1}{2}m\,(\dot{x}^2 + b^2\dot{\theta}^2 + 2b\dot{x}\dot{\theta}\cos\theta)$

La energía cinética de rotación es

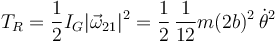
$T_R = \dfrac{1}{2} I_G |\vec{\omega}_{21}|^2 = \dfrac{1}{2}\, \dfrac{1}{12}m(2b)^2\,\dot{\theta}^2$

La energía cinética total es

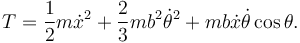
$T = \dfrac{1}{2}m\dot{x}^2 + \dfrac{2}{3}mb^2\dot{\theta}^2 + mb\dot{x}\dot{\theta}\cos\theta.$

La única fuerza conservartiva en el problema es la gravedad. Tomando como referencia de energía potencial gravitatoria la altura del punto $O$ tenemos

$U = U g = - m g b cosθ.$

2.3 Percusión

La velocidad del punto $C$ es

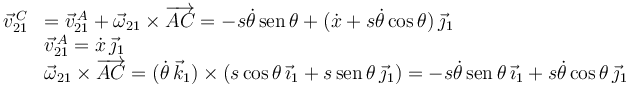
$\begin{array}{ll} \vec{v}^{\,C}_{21}& = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AC} = -s\dot{\theta}\,\mathrm{sen}\,\theta + (\dot{x} + s\dot{\theta}\cos\theta)\,\vec{\jmath}_1 \\ & \vec{v}^{\,A}_{21} = \dot{x}\,\vec{\jmath}_1\\ & \vec{\omega}_{21}\times\overrightarrow{AC} = (\dot{\theta}\,\vec{k}_1)\times (s\cos\theta\,\vec{\imath}_1 + s\,\mathrm{sen}\,\theta\,\vec{\jmath}_1) = -s\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + s\dot{\theta}\cos\theta\,\vec{\jmath}_1 \end{array}$

La función de Lagrange es

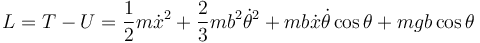
$L = T - U = \dfrac{1}{2}m\dot{x}^2 + \dfrac{2}{3}mb^2\dot{\theta}^2 + mb\dot{x}\dot{\theta}\cos\theta + mgb\cos\theta$

Como hay dos grados de libertad, tendremos dos ecuaciones de Lagrange percusivas

$\Delta p_x = \hat{Q}^{NC}_x, \qquad \Delta p_{\theta} = \hat{Q}^{NC}_{\theta}.$

Para la primera tenemos

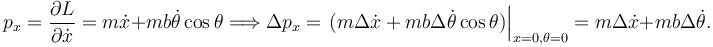
$p_x = \dfrac{\partial L}{\partial \dot{x}} = m\dot{x} + mb\dot{\theta}\cos\theta \Longrightarrow \Delta p_x = \left.(m\Delta\dot{x} + mb\Delta\dot{\theta}\cos\theta)\right|_{x=0, \theta=0} = m\Delta\dot{x} + mb\Delta\dot{\theta}.$

La percusión generalizada para la coordenada $x$ es

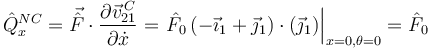
$\hat{Q}^{NC}_x = \vec{\hat{F}}\cdot\dfrac{\partial \vec{v}^{\,C}_{21}}{\partial\dot{x}} = \left.\hat{F}_0\,(-\vec{\imath}_1+\vec{\jmath}_1)\cdot(\vec{\jmath}_1)\right|_{x=0, \theta=0} =\hat{F}_0$

Obtenemos así la ecuación

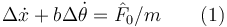
$\Delta\dot{x} + b\Delta\dot{\theta} = \hat{F}_0/m\qquad (1)$

Procedemos de manera similar para $θ$

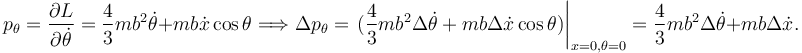
$p_{\theta} = \dfrac{\partial L}{\partial \dot{\theta}} = \dfrac{4}{3}mb^2\dot{\theta} + mb\dot{x}\cos\theta \Longrightarrow \Delta p_{\theta} = \left.(\dfrac{4}{3}mb^2\Delta\dot{\theta} + mb\Delta\dot{x}\cos\theta)\right|_{x=0, \theta=0} = \dfrac{4}{3}mb^2\Delta\dot{\theta} + mb\Delta\dot{x}.$

La percusión generalizada para la coordenada $θ$ es

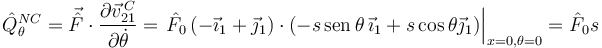
$\hat{Q}^{NC}_{\theta} = \vec{\hat{F}}\cdot\dfrac{\partial \vec{v}^{\,C}_{21}}{\partial\dot{\theta}} = \left.\hat{F}_0\,(-\vec{\imath}_1+\vec{\jmath}_1)\cdot(-s\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + s\cos\theta\vec{\jmath}_1)\right|_{x=0, \theta=0} =\hat{F}_0s$

Obtenemos así la ecuación

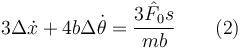
$3\Delta\dot{x} + 4b\Delta\dot{\theta} = \dfrac{3\hat{F}_0s}{mb} \qquad (2)$

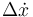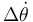Resolviendo para $\Delta\dot{x}$ y $\Delta\dot{\theta}$ obtenemos

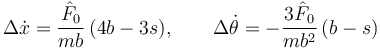
$\Delta\dot{x} = \dfrac{\hat{F}_0}{mb}\,(4b-3s), \qquad \Delta\dot{\theta} = -\dfrac{3\hat{F}_0}{mb^2}\,(b-s)$

Como la barra parte del reposo: 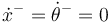$\dot{x}^- = \dot{\theta}^-=0$ . Por tanto

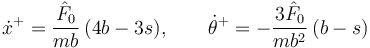
$\dot{x}^+ = \dfrac{\hat{F}_0}{mb}\,(4b-3s), \qquad \dot{\theta}^+ = -\dfrac{3\hat{F}_0}{mb^2}\,(b-s)$

La figura de la derecha muestra las percusiones que actúan sobre la barra, a saber, la percusión libre 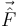$\vec{\hat{F}}$ y la percusión vincular 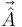$\vec{\hat{A}}$ . Aplicando el T.C.M Percusivo tenemos

$\Delta\vec{C} = \vec{\hat{F}} + \vec{\hat{A}} \Longrightarrow \vec{\hat{A}} = \Delta\vec{C} - \vec{\hat{F}}$

La variación de la cantidad de movimiento es

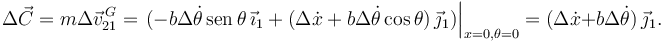
$\Delta\vec{C} = m\Delta\vec{v}^{\,G}_{21} = \left.(-b\Delta\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + (\Delta\dot{x} + b\Delta\dot{\theta}\cos\theta)\,\vec{\jmath}_1)\right|_{x=0,\theta=0} = (\Delta\dot{x} + b\Delta\dot{\theta})\,\vec{\jmath}_1.$

Utilizando la solución calculada antes tenemos

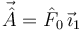
$\vec{\hat{A}} = \hat{F}_0\,\vec{\imath}_1$

2.4 Movimiento de $A$ en función de $s$

La velocidad de $A$ justo después de la percusión es

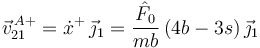
$\vec{v}^{\,A+}_{21} = \dot{x}^+\,\vec{\jmath}_1 = \dfrac{\hat{F}_0}{mb}\,(4b-3s)\,\vec{\jmath}_1$

Vemos que si $s = s p = 4 b / 3$ esta velocidad es nula. Ese valor de $s$ indica la posición del centro de percusión de $A$ . Si $s < s p$ (la parte de arriba de la barra) el punto $A$ se mueve hacia la derecha. Si $s > s p$ (la parte de abajo de la barra) el punto $A$ se mueve hacia la izquierda.

Percusión sobre una barra vertical (Feb. 2020)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducción cinemática

2.2 Energía cinética y potencial

2.3 Percusión

2.4 Movimiento de $A$ en función de $s$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Percusión sobre una barra vertical (Feb. 2020)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducción cinemática

2.2 Energía cinética y potencial

2.3 Percusión

2.4 Movimiento de A en función de s

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.4 Movimiento de $A$ en función de $s$