Partícula suspendida de dos muelles

De Laplace

1 Enunciado

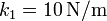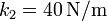Una partícula de peso 2 N cuelga del techo suspendida de dos muelles en paralelo, ambos de longitud natural 15 cm. El muelle 1 tiene constante $k_1=10\,\mathrm{N}/\mathrm{m}$ y el 2 $k_2 = 40\,\mathrm{N}/\mathrm{m}$ .

En el equilibrio, ¿cuál es la distancia de la partícula al techo?
Si, estando en la posición anterior, se corta la unión de la masa con el muelle 2, ¿cuánto vale la amplitud de las oscilaciones resultantes?

2 Distancia de equilibrio

Al estar suspendida simultáneamente de los dos muelles, las fuerzas elásticas se suman. Puesto que todas las fuerzas son verticales podemos emplear cantidades escalares y escribir

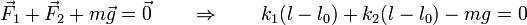
$\vec{F}_1+\vec{F}_2+m\vec{g}=\vec{0}\qquad\Rightarrow\qquad k_1(l-l_0)+k_2(l-l_0) - m g = 0$

donde, a la hora de escribir los signos hay que tener cuidado de razonar previamente el sentido de las fuerzas. En este caso, si la longitud del muelle es mayor que la natural, la fuerza elástica va hacia arriba.

En este caso los dos muelles tienen la misma longitud natural y ambos se estiran la misma cantidad, lo que nos da simplemente

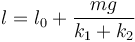
$l = l_0 +\frac{mg}{k_1+k_2}$

esto es, la asociación se comporta como un solo resorte de constante $k = k 1 + k 2$ . El valor numérico de esta distancia es

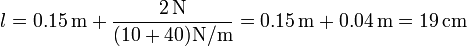
$l = 0.15\,\mathrm{m} + \frac{2\,\mathrm{N}}{(10+40)\mathrm{N}/\mathrm{m}} = 0.15\,\mathrm{m}+0.04\,\mathrm{m}=19\,\mathrm{cm}$

3 Amplitud de las oscilaciones

Cuando se corta la unión con el muelle 2, la fuerza elástica disminuye. El peso supera a esta fuerza y la masa comienza a descender. Al hacerlo, aumenta la elongación del muelle 1 y la fuerza elástica que produce, llegando a superar al peso. La masa describe entonces un movimiento armónico simple vertical con ecuación de movimiento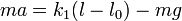 $ma = k_1(l-l_0) - mg\,$

cuya posición de equilibrio se encuentra en

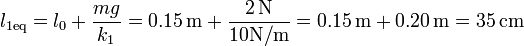
$l_{1\mathrm{eq}}=l_0+\frac{mg}{k_1}=0.15\,\mathrm{m}+\frac{2\,\mathrm{N}}{10\mathrm{N}/\mathrm{m}} = 0.15\,\mathrm{m}+0.20\,\mathrm{m}=35\,\mathrm{cm}$

Inicialmente se encontraba en la posición calculada en el apartado anterior. Puesto que parte del reposo, la amplitud de las oscilaciones resultantes será la diferencia entre la posición de partida y la nueva posición de equilibrio

$A = l_{1\mathrm{eq}}-l_{10}=\left(l_0+\frac{mg}{k_1}\right)-\left(l_0+\frac{mg}{k_1+k_2}\right) = 35\,\mathrm{cm}-19\,\mathrm{cm}=16\,\mathrm{cm}$

Partícula suspendida de dos muelles

De Laplace

1 Enunciado

2 Distancia de equilibrio

3 Amplitud de las oscilaciones

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES