Partícula sobre plano inclinado con dos muelles, Noviembre 2015 (G.I.C.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una masa $m$ está obligada a permanecer sobre un plano horizontal que forma un ángulo $π / 4$ con la horizontal. La masa está conectada a dos muelles con longitud natural nula y constante elástica $k$ , anclados en los puntos $A$ y $B$ de la figura. El punto $A$ desliza sobre el eje $O X$ de modo que el muelle anclado en él permanece vertical en todo instante. El sistema está diseñado de modo que 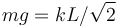$mg = kL/\sqrt{2}$ .

Encuentra la expresión vectorial de las fuerzas que ejercen los muelles, expresadas en los ejes de la figura
Suponiendo que todos los contactos son lisos, calcula la posición de equilibrio $d 0$
Añadimos ahora rozamiento entre la partícula y el plano. Dada una posición $d m$ , ¿cuánto vale el módulo de la fuerza de rozamiento?
Si el coeficiente de rozamiento estático es $μ$ , ¿cuál es el rango de posiciones posibles de equilibrio de la partícula?

2 Solución

2.1 Fuerzas de los muelles

Son dos muelles con longitud natural nula, por lo que las expresiones vectoriales de las fuerzas son

$\vec{F}_A = -k\overrightarrow{AP}, \qquad \vec{F}_B = -k\overrightarrow{BP}.$

Vamos a construir los vectores que aparecen. Observando la figura vemos que

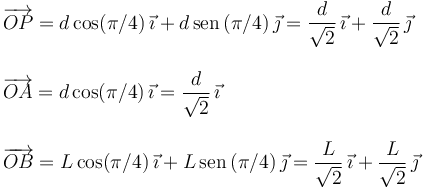
$\begin{array}{l} \overrightarrow{OP} = d\cos(\pi/4)\,\vec{\imath} + d\,\mathrm{sen}\,(\pi/4)\,\vec{\jmath} = \dfrac{d}{\sqrt{2}}\,\vec{\imath} + \dfrac{d}{\sqrt{2}}\,\vec{\jmath} \\ \\ \overrightarrow{OA} = d\cos(\pi/4)\,\vec{\imath} = \dfrac{d}{\sqrt{2}}\,\vec{\imath} \\ \\ \overrightarrow{OB} = L\cos(\pi/4)\,\vec{\imath} + L\,\mathrm{sen}\,(\pi/4)\,\vec{\jmath} = \dfrac{L}{\sqrt{2}}\,\vec{\imath} + \dfrac{L}{\sqrt{2}}\,\vec{\jmath} \end{array}$

Entonces

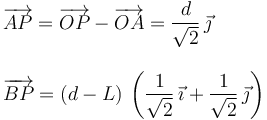
$\begin{array}{l} \overrightarrow{AP} = \overrightarrow{OP} - \overrightarrow{OA} = \dfrac{d}{\sqrt{2}}\,\vec{\jmath} \\ \\ \overrightarrow{BP} = (d-L)\,\left(\dfrac{1}{\sqrt{2}}\,\vec{\imath} + \dfrac{1}{\sqrt{2}}\,\vec{\jmath}\right) \end{array}$

Y las fuerzas son

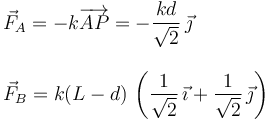
$\begin{array}{l} \vec{F}_A = -k\overrightarrow{AP} = -\dfrac{kd}{\sqrt{2}}\,\vec{\jmath} \\ \\ \vec{F}_B = k(L-d)\,\left(\dfrac{1}{\sqrt{2}}\,\vec{\imath} + \dfrac{1}{\sqrt{2}}\,\vec{\jmath}\right) \end{array}$

2.2 Posición de equilibrio con contactos lisos

La figura de la derecha muestra las fuerzas que actúan sobre la partícula cuando el vínculo es liso: las dos fuerzas de los muelles, el peso y la fuerza de ligadura del plano inclinado, perpendicular a él. Expresamos estas fuerzas en los ejes indicados

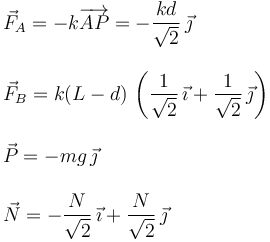
$\begin{array}{l} \vec{F}_A = -k\overrightarrow{AP} = -\dfrac{kd}{\sqrt{2}}\,\vec{\jmath} \\ \\ \vec{F}_B = k(L-d)\,\left(\dfrac{1}{\sqrt{2}}\,\vec{\imath} + \dfrac{1}{\sqrt{2}}\,\vec{\jmath}\right) \\ \\ \vec{P} = -mg\,\vec{\jmath} \\ \\ \vec{N} = -\dfrac{N}{\sqrt{2}}\,\vec{\imath} + \dfrac{N}{\sqrt{2}}\,\vec{\jmath} \end{array}$

La condición de equilibrio es que la suma total de fuerzas sea nula:

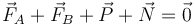
$\vec{F}_A + \vec{F}_B + \vec{P} + \vec{N} = \vec{0}$

Esta ecuación vectorial nos proporciona dos ecuaciones escalares, una por cada componente:

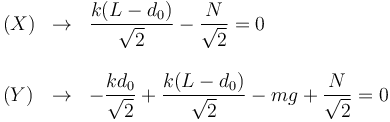
$\begin{array}{lcl} (X) & \to & \dfrac{k(L-d_0)}{\sqrt{2}} - \dfrac{N}{\sqrt{2}} = 0 \\ \\ (Y) & \to & -\dfrac{kd_0}{\sqrt{2}} + \dfrac{k(L-d_0)}{\sqrt{2}} -mg + \dfrac{N}{\sqrt{2}} = 0 \end{array}$

Tenemos dos incógnitas: $d 0$ y $N$ . Restando las dos ecuaciones eliminamos $N$ y obtenemos una ecuación para $d 0$ . Utilizando que, según el enunciado, 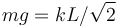$mg = kL/\sqrt{2}$ , nos queda

$d 0 = L / 3$

La componente de la fuerza normal se obtiene ahora de la primera ecuación

$N = 2 K L / 3$

2.3 Inclusión de rozamiento

Al incluir el rozamiento entre la partícula y el plano, hemos de añadir otra fuerza tangente al plano, como se indica en la figura. La expresión de esta fuerza en los ejes es

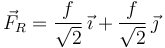
$\vec{F}_R = \dfrac{f}{\sqrt{2}}\,\vec{\imath} + \dfrac{f}{\sqrt{2}}\,\vec{\jmath}$

La condición de equilibrio ahora es

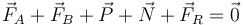
$\vec{F}_A + \vec{F}_B + \vec{P} + \vec{N} + \vec{F}_R = \vec{0}$

De nuevo obtenemos dos ecuaciones escalares, una por componente

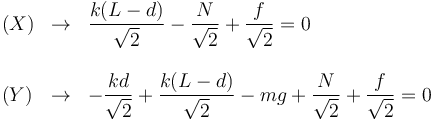
$\begin{array}{lcl} (X) & \to & \dfrac{k(L-d)}{\sqrt{2}} - \dfrac{N}{\sqrt{2}} + \dfrac{f}{\sqrt{2}} = 0 \\ \\ (Y) & \to & -\dfrac{kd}{\sqrt{2}} + \dfrac{k(L-d)}{\sqrt{2}} -mg + \dfrac{N}{\sqrt{2}} + \dfrac{f}{\sqrt{2}}= 0 \end{array}$

Ahora tenemos tres incógnitas, a saber, $d$ , $N$ y $f$ . Pero sólo tenemos dos ecuaciones. Esto se debe a que, al incluir el rozamiento, hay varias posiciones posibles de equilibro, por lo que el sistema de ecuaciones no tiene solución única. Sin embargo, para una posición fijada $d m$ , si podemos averiguar las componentes, y por tanto los módulos, de las fuerzas de ligadura y de rozamiento. Si $d = d m$ es un dato, restamos las dos ecuaciones para eliminar $N$ . De este modo obtenemos

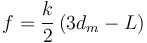
$f = \dfrac{k}{2}\,(3d_m-L)$

y para $N$ tenemos

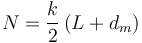
$N=\dfrac{k}{2}\,(L+d_m)$

Los vectores correspondientes son

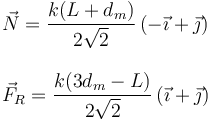
$\begin{array}{l} \vec{N} = \dfrac{k(L+d_m)}{2\sqrt{2}}\,(-\vec{\imath} + \vec{\jmath}) \\ \\ \vec{F}_R = \dfrac{k(3d_m-L)}{2\sqrt{2}}\,(\vec{\imath} + \vec{\jmath}) \end{array}$

Ahora podemos averiguar el intervalo de posiciones posibles de equilibro. Dada una posición $d m$ , para que el equilibrio sea posible debe cumplirse

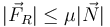
$|\vec{F}_R|\leq \mu|\vec{N}|$

siendo $μ$ el coeficiente de rozamiento estático. Los módulos son

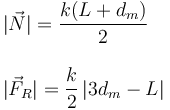
$\begin{array}{l} |\vec{N}| = \dfrac{k(L+d_m)}{2} \\ \\ |\vec{F}_R| = \dfrac{k}{2}\,|3d_m-L| \end{array}$

Hemos de tratar con cuidado el módulo de la fuerza de rozamiento. La expresión dentro del valor absoluto puede ser positiva o negativa, según los valores relativos de $d m$ y $L$ . Consideramos dos situaciones

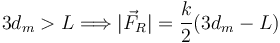
$3d_m>L \Longrightarrow |\vec{F}_R| = \dfrac{k}{2}(3d_m-L)$

En este caso para que la posición pueda ser de equilibrio debe cumplirse

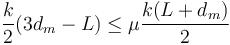
$\dfrac{k}{2}(3d_m-L) \leq \mu\dfrac{k(L+d_m)}{2}$

De aquí obtenemos una condición de máximo para $d m$

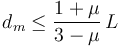
$d_m \leq \dfrac{1+\mu}{3-\mu}\,L$

La otra situación ocurre cuando

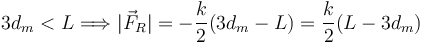
$3d_m<L \Longrightarrow |\vec{F}_R| = -\dfrac{k}{2}(3d_m-L) = \dfrac{k}{2}(L-3d_m)$

Ahora la condición de equilibrio se traduce en

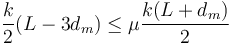
$\dfrac{k}{2}(L-3d_m) \leq \mu\dfrac{k(L+d_m)}{2}$

Y obtenemos una condición de mínimo para $d m$

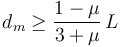
$d_m \geq \dfrac{1-\mu}{3+\mu}\,L$

Entonces, para que una posición $d m$ pueda ser de equilibrio, debe cumplirse la condición

$d_m \in \left[\dfrac{1-\mu}{3+\mu}\,L, \dfrac{1+\mu}{3-\mu}\,L\right]$

Físicamente, el hecho de tener que considerar dos situaciones para el módulo de la fuerza de rozamiento corresponde a que el sentido de la fuerza de rozamiento no está determinado a priori. Si el muelle de arriba domina la fuerza de rozamiento apunta en el sentido negativo del eje $X$ . Si dominan el peso y el muelle de abajo, la fuerza de rozamiento apunta hacia el sentido positivo del eje $X$ .

Partícula sobre plano inclinado con dos muelles, Noviembre 2015 (G.I.C.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Fuerzas de los muelles

2.2 Posición de equilibrio con contactos lisos

2.3 Inclusión de rozamiento

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES