Partícula recorriendo una espiral, Enero 2015 (G.I.C.)
De Laplace
Contenido |
1 Enunciado
Una partícula de masa m describe una espiral plana con un vector de posición en coordenadas polares 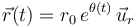 , siendo θ(t) = ωt. Tanto r0 como ω son constantes.
, siendo θ(t) = ωt. Tanto r0 como ω son constantes.
- Calcula el momento cinético de la partícula respecto del origen.
- Calcula el momento respecto del origen de la fuerza neta que actúa sobre la partícula.
2 Solución
2.1 Momento cinético
El vector de posición de la partícula es, en polares:
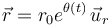
Derivamos respecto al tiempo para obtener la velocidad
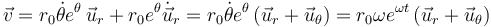
Hemos usado que θ = ωt y 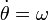
El momento cinético respecto del origen es
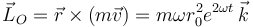
2.2 Momento de la fuerza neta
El teorema del momento cinético dice
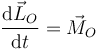
siendo 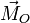 el momento de la fuerza neta respecto del punto O. Derivando en la expresión del apartado anterior tenemos
el momento de la fuerza neta respecto del punto O. Derivando en la expresión del apartado anterior tenemos






