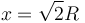Partícula que sale despedida de una semiesfera (GIE)

De Laplace

1 Enunciado

Una partícula de masa m se encuentra en lo alto de una cúpula hemisférica de radio R, sobre la cual la masa puede deslizar sin rozamiento. La semiesfera está rígidamente unida a una superficie horizontal. La masa está sometida a la acción del peso. Estando en esta posición se le comunica una velocidad horizontal de rapidez v₀

1. Determine el punto en el que la masa despega de la superficie esférica, dando el ángulo θ que el vector de posición relativa al centro de la esfera forma con la vertical.
2. ¿Cuál es el valor mínimo de v₀ para que la partícula despegue directamente de la superficie, sin deslizar sobre ella?
3. Para este valor mínimo de v₀ determine la distancia al centro de la semiesfera del punto de la superficie horizontal en el que impacta la partícula.

2 Separación

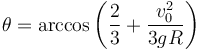
3 Velocidad mínima

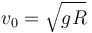
4 Punto de impacto