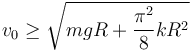De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

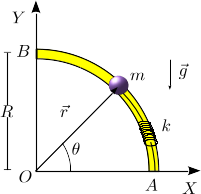
Una partícula de masa $m$ está engarzada en un aro de radio $R$ . El contacto entre la partícula y el aro es liso. La partícula está conectada a un muelle de constante elástica $k$ y longitud natural nula. El otro extremo del muelle está anclado en el punto $A$ . En el instante inicial la partícula se encuentra en el punto $A$ y se le comunica una velocidad vertical de módulo $v 0$ .

Encuentra la expresión de la energía mecánica del muelle en todo instante.
Calcula el momento cinético de la partícula cuando $θ = π / 4$ .
¿Cuál es el valor mínimo de $v 0$ para que la partícula llegue hasta el punto $B$ ?

Nota: La energía potencial elástica del muelle tiene la expresión $U k = k l 2 / 2$ , siendo $l$ su longitud.

2 Solución

2.1 Análisis previo

Las fuerzas que actúan sobre la partícula son el peso, la fuerza elástica del muelle y la fuerza vincular normal que el aro ejerce sobre ella. Las dos primeras son conservativas y la última, aunque no conservativa, no realiza trabajo. Es decir, la energía mecánica de la partícula se conserva a lo largo de su movimiento.

2.2 Expresión de la energía mecánica

La energía cinética es

$T = \dfrac{1}{2}mv^2,$

donde $v$ es la rapidez de la partícula.

La energía potencial gravitatoria puede escribirse

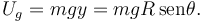
$U_g = mgy = mgR\,\mathrm{sen}\theta.$

Hemos escogido como origen de energía potencial gravitatoria la altura $y = 0$ .

La energía potencial elástica es

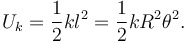
$U_k = \dfrac{1}{2}kl^2 = \dfrac{1}{2}kR^2\theta^2.$

La energía mecánica es

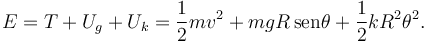
$E = T + U_g + U_k = \dfrac{1}{2}mv^2 + mgR\,\mathrm{sen}\theta + \dfrac{1}{2}kR^2\theta^2.$

En el instante inicial tenemos $v = v 0$ y $θ = 0$ . Entonces

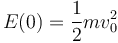
$E(0) = \dfrac{1}{2}mv_0^2$

Como la energía mecánica se conserva, en cualquier instante del movimiento se cumple

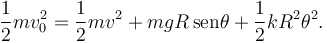
$\dfrac{1}{2}mv_0^2 = \dfrac{1}{2}mv^2 + mgR\,\mathrm{sen}\theta + \dfrac{1}{2}kR^2\theta^2.$

2.3 Momento cinético

El momento cinético (o angular) de una partícula respecto a un punto es

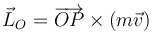
$\vec{L}_O = \overrightarrow{OP}\times(m\vec{v})$

Cuando $θ = π / 4$ tenemos

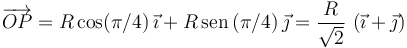
$\overrightarrow{OP} = R\cos(\pi/4)\,\vec{\imath} + R\,\mathrm{sen}\,(\pi/4)\,\vec{\jmath} = \dfrac{R}{\sqrt{2}}\,\left(\vec{\imath} + \vec{\jmath}\right)$

Para el módulo de la velocidad en este instante, $v 1$ , tenemos, de la conservación de energía mecánica

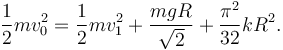
$\dfrac{1}{2}mv_0^2 = \dfrac{1}{2}mv_1^2 + \dfrac{mgR}{\sqrt{2}} + \dfrac{\pi^2}{32}kR^2.$

Por tanto

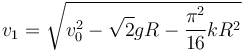
$v_1 = \sqrt{v_0^2 - \sqrt{2}gR - \dfrac{\pi^2}{16}kR^2}$

Del dibujo vemos que el vector velocidad es

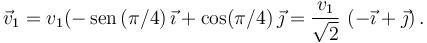
$\vec{v}_1 = v_1 (-\,\mathrm{sen}\,(\pi/4)\,\vec{\imath} + \cos(\pi/4)\,\vec{\jmath} = \dfrac{v_1}{\sqrt{2}}\,\left(-\vec{\imath} + \vec{\jmath}\right).$

Aquí, $v 1$ viene dado por la expresión que hemos obtenido antes.

El momento cinético pedido es

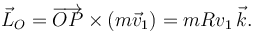
$\vec{L}_O = \overrightarrow{OP}\times(m\vec{v}_1) = mRv_1\,\vec{k}.$

2.4 Velocidad mínima

Utilizando de nuevo la expresión obtenida de la conservación de la energía mecánica vemos que, cuando $θ = π / 2$ se cumple

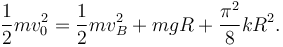
$\dfrac{1}{2}mv_0^2 = \dfrac{1}{2}mv_B^2 + mgR+ \dfrac{\pi^2}{8}kR^2.$

La rapidez en el punto $B$ es

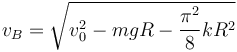
$v_B = \sqrt{v_0^2 - mgR - \dfrac{\pi^2}{8}kR^2}$

Para que llegue arriba esta rapidez debe ser mayor o igual que cero. Entonces la condición es

$v_0\geq \sqrt{mgR + \dfrac{\pi^2}{8}kR^2}$

Partícula engarzada en un hilo circular con un muelle, Enero 2018 (G.I.E.R.M.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Análisis previo

2.2 Expresión de la energía mecánica

2.3 Momento cinético

2.4 Velocidad mínima

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES