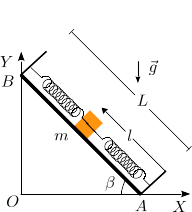
Partícula en plano inclinado con dos muelles (Ene. 2018 G.I.C.)
De Laplace
Contenido |
1 Enunciado
Una masa m desliza sin rozamiento sobre un plano inclinado un ángulo β respecto a la horizontal. La barra está conectada a dos muelles ideales como se indica en la figura. Los muelles tienen constante elástica k y longitud natural nula. El muelle se ajusta de modo que k = mg / L. El ángulo β cumple

- Escribe la expresión que da la energía mecánica de la partícula para cualquier punto del plano.
- En el instante inicial la partícula está en el punto A y se le comunica una velocidad de módulo v0 dirigida hacia arriba. ¿Que valor mínimo debe tener v0 para que la partícula llegue hasta el punto B?
- Repite el cálculo del apartado anterior si hay un rozamiento entre la partícula y el plano con coeficiente de rozamiento dinámico μ = 0.5.
2 Solución
2.1 Análisis previo
En los dos primeros apartados no hay fuerza de rozamiento. Las fuerzas que actúan son el peso, las de las dos muelles y la fuerza vincular normal del plano. Las tres primeras son conservativas. La fuerza vincular no lo es, pero no hace trabajo pues es siempre perpendicular a la velocidad de la partícula. Entonces la energía mecánica se conserva en los dos primeros apartados.
En el tercer apartado se tiene en cuenta la fuerza de rozamiento, que es no conservativa y sí hace trabajo. Por tanto la energía mecánica no se conserva en este apartado, pero se puede calcular su variación, pues la fuerza de rozamiento es constante durante el movimiento de la partícula.
2.2 Energía mecánica
La energía cinética es

donde v es el módulo de la velocidad de la partícula.
Hay una energía potencial por cada fuerza conservativa que actúa. Tomando como referencia de energía potencial gravitatoria la altura y = 0 tenemos

La coordenada l indica la posición de la partícula sobre el plano inclinado, siendo l = 0 el punto A.
Para los muelles tenemos

La energía mecánica es
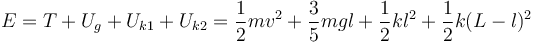
Usando la condición k = mg / L tenemos

2.3 Velocidad inicial para que llegue a B
En el instante inicial tenemos

con lo que la energía mecánica inicial es
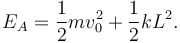
Al no haber rozamiento la energía mecánica se conserva, con lo que en el punto B tenemos (l = L)

Como las dos energías han de ser iguales, la rapidez en el punto B es

La condición para que llegue arriba es  , por tanto
, por tanto

2.4 Velocidad mínima con fuerza de rozamiento
Ahora no se conserva la energía mecánica, pero podemos calcular su variación. Tenemos
EB − EA = WR.
La expresiones de la energía mecánica en A y B son similares a las de antes. El trabajo de rozamiento se calcula como sigue.
La figura de la derecha muestra las fuerzas que actúan sobre la masa. En este apartado nos interesa sólo la de rozamiento. Como la partícula se mueve respecto del plano, el régimen de rozamiento es dinámico, por lo que se cumple

Del dibujo vemos que la fuerza normal debe cancelar la componente del peso perpendicular al plano inclinado, es decir
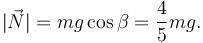
Entonces la fuerza de rozamiento es, en módulo,
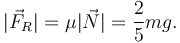
La fuerza de rozamiento es constante durante el movimiento de la partícula y esta realiza un movimiento rectilíneo. Además, la fuerza de rozamiento se opone siempre a la velocidad, Por tanto, el trabajo realizado por el rozamiento es

Entonces tenemos

Aplicamos el Teorema de la energía mecánica

Para que la partícula llegue arriba este valor tiene que ser mayor o igual que cero, por tanto

Este valor mínimo es mayor que el que se obtiene sin rozamiento. Esto es lógico, pues el rozamiento hace que se pierda energía mecánica en el trayecto, por lo que su valor inicial debe ser mayor.