Partícula en parábola con muelle

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Altura máxima
- 2.2 Relación entre k y m

1 Enunciado

(Final, Julio 2009, T1 aplicación)

Una partícula material de masa $m$ está ensartada en una parábola contenida en un plano vertical, de ecuación $y = x 2 / a$ , por la que desliza sin rozamiento. La partícula está sometida a la acción de la gravedad y de un resorte de longitud natural nula y constante recuperadora $k$ . El otro extremo del resorte está conectado a un punto fijo $A$ de coordenadas $A (x = 0; y = a)$ . En el instante inicial la partícula se encuentra en reposo en el punto más bajo de la parábola [punto $O (x = 0; y = 0)$ ].

Supongamos que una perturbación desplaza infinitesimalmente la partícula en el sentido positivo del eje $X$ . Si la partícula se sigue moviendo hacia arriba a lo largo de la parábola, ¿que altura máxima puede alcanzar?
¿Qué relación han de verificar la masa $m$ y la constante $k$ para que pueda producirse el movimiento anterior?

2 Solución

2.1 Altura máxima

Para encontrar la altura máxima basta aplicar el principio de conservación de la energía mecánica. En el sistema hay dos fuerzas conservativas, la del muelle y la gravedad. La energía potencial es

$U=\frac{1}{2}kl^2+mgy$

Aquí, $l$ es la distancia de la partícula hasta el punto de anclaje del muelle, el punto $A$ . Para la energía potencial gravitatoria hemos considerado el origen de energía en $y = 0$ , es decir, la posición original de la partícula.

Como la partícula se mueve siempre sobre la parábola, la distancia entre ella y el punto $A$ es

l 2 = (x - x A) 2 + (y - y A) 2 = x 2 + (y - a) 2 = a y + (y - a) 2 = y 2 - a y + a 2

Así, pues la energía potencial total es

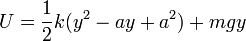
$U=\frac{1}{2}k(y^2-ay+a^2)+mgy$

En la situación inicial la partícula está en reposo en el vértice de la parábola. Por tanto, la energía mecánica vale

$E = U(y=0) = \frac{1}{2}ka^2$

En el vértice de la parábola la fuerza del muelle y la de la gravedad se compensan exactamente. Sin embargo, puede ser un punto de equilibrio inestable, pues la mas pequeña desviación a un lado o al otro provoca que el muelle tire hacia arriba de la partícula. (En un experimento real sería imposible colocar la partícula exactamente en el vértice, así que ese pequeño desplazamiento siempre existirá). Al ir subiendo el muelle acelera la partícula, con lo que aumenta su energía cinética, pero la gravedad, e incluso el muelle para $y > a$ , intentan frenarla. Para un valor cualquiera de $y$ podemos obtener el módulo de la velocidad a partir de la conservación de la energía mecánica

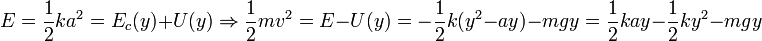
$E=\frac{1}{2}ka^2=E_c(y)+U(y)\Rightarrow \frac{1}{2}mv^2=E-U(y)=-\frac{1}{2}k(y^2-ay)-mgy=\frac{1}{2}kay-\frac{1}{2}ky^2-mgy$

Los puntos de retorno son aquellos en que la velocidad se anula, es decir

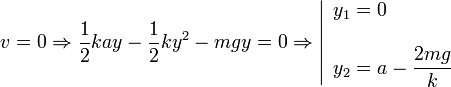
$v= 0\Rightarrow \frac{1}{2}kay-\frac{1}{2}ky^2-mgy=0\Rightarrow \left| \begin{array}{l} y_1=0\\ \\\displaystyle y_2=a-\frac{2mg}{k} \end{array} \right.$

El primer punto corresponde al vértice de la parábola. El segundo es la altura a la que la partícula se frena y vuelve a descender

2.2 Relación entre $k$ y $m$

Para que el valor de $y 2$ del punto de retorno que hemos calculado en el apartado anterior sea posible, debe ocurrir 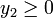$y_2\geq0$ . Esto impone la condición

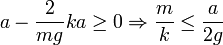
$a-\frac{2}{mg}{ka}\geq 0\Rightarrow \frac{m}{k}\leq\frac{a}{2g}$

Si la partícula es demasiado pesada ( $m$ grande) o el muelle demasiado débil ( $k$ pequeña), el resorte no es capaz de levantar a la partícula.

Partícula en parábola con muelle

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Altura máxima

2.2 Relación entre $k$ y $m$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Partícula en parábola con muelle

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Altura máxima

2.2 Relación entre k y m

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.2 Relación entre $k$ y $m$