De Laplace

1 Enunciado

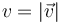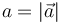Una partícula se mueve describiendo una trayectoria cuyo radio de curvatura $R κ$ es proporcional a la distancia $s$ que aquélla ha recorrido sobre la trayectoria. Además, se comprueba que el módulo de la velocidad de la partícula (celeridad), $v=|\vec{v}|$ , es proporcional a la raíz cuadrada del valor de dicha distancia $s$ . ¿Cómo es el módulo de la aceleración instantánea de la partícula, $a=|\vec{a}|$ ?

2 Solución

Nos dice el enunciado que el radio de curvatura es de la forma

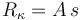
$R_{\kappa} = A\,s$

siendo $A$ una constante. Y la celeridad es

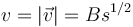
$v = |\vec{v}| = B s^{1/2}$

siendo $B$ también constante.

El radio de curvatura se relaciona con la aceleración normal

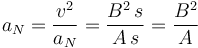
$a_N = \dfrac{v^2}{a_N} = \dfrac{B^2\,s}{A\,s} = \dfrac{B^2}{A}$

también constante.

La aceleración tangencial se relaciona con la derivada del módulo de la velocidad respecto del tiempo. Usamos la regla de la cadena para relacionarlo con la derivada respecto del parámetro arco

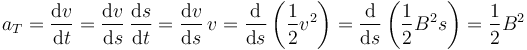
$a_T = \dfrac{\mathrm{d}v}{\mathrm{d}t} = \dfrac{\mathrm{d}v}{\mathrm{d}s}\,\dfrac{\mathrm{d}s}{\mathrm{d}t} = \dfrac{\mathrm{d}v}{\mathrm{d}s}\,v = \dfrac{\mathrm{d} }{\mathrm{d}s}\left(\dfrac{1}{2}v^2\right) = \dfrac{\mathrm{d} }{\mathrm{d}s}\left(\dfrac{1}{2}B^2s\right) = \dfrac{1}{2}B^2$