Partícula con cuerda deslizando sobre punto de una circunferencia (Nov. 2017 G.I.C.)
De Laplace
Contenido |
1 Enunciado
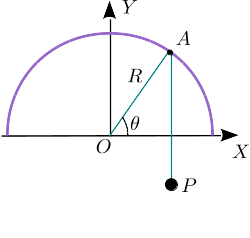
Una partícula de masa m cuelga de una cuerda inextensible sin masa. La cuerda desliza sobre el punto A. A su vez, este punto se mueve sobre una circunferencia de radio R. La longitud de la cuerda cambia en el tiempo según la ley l(t) = 2R(1 − Ωt). En el instante inicial el punto A se encontraba sobre el eje X, a la derecha del origen.
- Escribe el vector de posición de la partícula
- El punto A realiza un movimiento circular uniforme con una aceleración que cumple
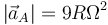 . Encuentra la velocidad de la partícula P.
. Encuentra la velocidad de la partícula P.
- Calcula el vector normal de la trayectoria de la partícula y su curvatura en el instante t = 0.
2 Solución
2.1 Vector de posición
El vector de posición de la partícula P puede escribirse como
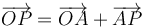
Tenemos

Por otra parte
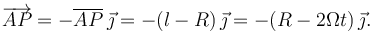
Entonces
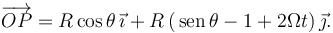
2.2 Velocidad de la partícula
El punto A realiza un movimiento circular uniforme. Entonces

Tenemos

Y derivando otra vez
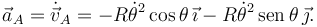
El módulo de la aceleración es
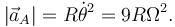
Entonces

Hemos usado que θ(0) = 0, como dice el enunciado, pues en el instante inicial el punto A estaba sobre el eje X a la derecha del origen.
Entonces, para el punto P tenemos
![\begin{array}{l}
\vec{v}_P = R\Omega \,[-3\,\mathrm{sen}\,\theta\,\vec{\imath} + (2+3\cos\theta)\,\vec{\jmath}],\\
\vec{a}_P = -9R\Omega^2\,(\cos\theta\,\vec{\imath} + \mathrm{sen}\,\theta\,\vec{\jmath}).
\end{array}](/wiki/images/math/1/1/b/11bd783ed48739deea4c6d9d6f86c6e0.png)
2.3 Vector normal y curvatura en el instante inicial
En t = 0 tenemos θ = 0. La velocidad y aceleración del punto P en ese instante son
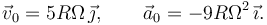
Como son perpendiculares, la aceleración sólo tiene componente normal. Es decir

El vector normal es
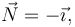
y la curvatura es