Oscilaciones acopladas (CMR)

De Laplace

Contenido

1 Introducción
2 Sistema simétrico
3 Caso general de dos osciladores
4 El caso con rozamiento
- 4.1 Solución artesanal
- 4.2 Solución sistemática
5 Oscilaciones forzadas

1 Introducción

En un sistema real existen diferentes mecanismos que producen oscilaciones, siendo raro que se pueda describir un sólido real como un solo oscilador armónico. Esas diferentes formas de oscilación (modos) pueden superponerse y si son no lineales, incluso afectarse mutuamente.

En la respuesta a una excitación oscilante, un sistema real puede mostrar diferentes frecuencias de resonancia, según el modo que se excite.

Consideremos, como ejemplo sencillo, el caso de dos masas $m 1$ y $m 2$ de las cuales la primera está unida a una pared por un resorte horizontal de constante $k 1$ y la segunda a la primera por uno de constante $k 2$ .

Es fácil ver que este sistema puede tener conductas muy diferentes dependiendo de los valores de los parámetros.

Si 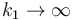$k_1\to \infty$ el primer muelle se convierte en una varilla rígida y no deja moverse a la primera masa.
Si 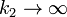$k_2\to\infty$ es el segundo muelle el que se comporta como una barra y las dos masas se mueven al únisono.
Si 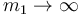$m_1\to\infty$ la inercia de la primera masa le impide moverse.
Si 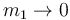$m_1\to 0$ los dos resortes en serie se comportan como uno solo.

Este caso posee una solución general que se puede hallar de forma sistemática, como veremos, pero que no es trivial. Consideraremos previamente un sistema más sencillo para ilustrar los aspectos principales.

2 Sistema simétrico

Supongamos dos masa iguales, $m$ , situadas sobre una superficie horizontal sin rozamiento, unidas a paredes enfrentadas que distan $b$ por resortes también iguales de constante k y longitud natural $l 0$ . Las dos masas están unidas entre si por otro resorte de constante K y longitud natural $L 0$ .

Se trata de estudiar la dinámica de este sistema para distintos valores de las constantes y diferentes condiciones iniciales.

2.1 Ecuaciones de movimiento

Puesto que el movimiento es a lo largo de la recta que une las dos masas, podemos prescindir de los vectores y emplear magnitudes escalares.

La masa de la izquierda (masa 1) experimenta una fuerza por cada resorte conectada a ella, de forma que

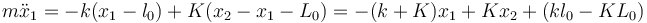
$m\ddot{x}_1 = -k(x_1-l_0)+K(x_2-x_1-L_0)= -(k+K)x_1+K x_2 +(kl_0-KL_0)$

y de manera análoga ocurre con la masa 2

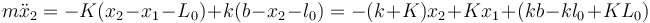
$m\ddot{x}_2 = -K(x_2-x_1-L_0)+k(b-x_2-l_0)= -(k+K)x_2+K x_1 +(kb-kl_0+KL_0)$

2.2 Posición de equilibrio

En primer lugar determinamos las posiciones de equilibrio de las dos masas. Para ello suponemos que se anulan las aceleraciones y queda el sistema

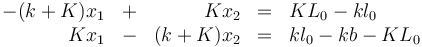
$\begin{array}{rcrcl}-(k+K)x_1 & + & K x_2 & = & KL_0-kl_0 \\ K x_1 & - & (k+K)x_2& = & kl_0 - kb - K L_0 \end{array}$

Sumando las dos ecuaciones obtenemos

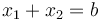
$x_1+x_2 = b\,$

que nos dice que el punto medio entre las dos masas es el central del sistema y que están situadas simétricamente respecto a este punto. Despejando de aquí y sustituyendo

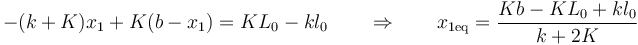
$-(k+K)x_1 + K (b-x_1) = KL_0-kl_0 \qquad\Rightarrow\qquad x_{1\mathrm{eq}} = \frac{Kb - KL_0 + kl_0}{k+2K}$

Podemos, a modo de comprobación, tomar límites destacados.

Si 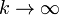$k\to\infty$ esta posición tiende a

$x_{1\mathrm{eq}}\xrightarrow{k\to\infty}\ l_0$

que nos dice que los muelles exteriores son rígidos y las masas están a una distancia fijada

Si 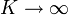$K\to\infty$ el límite es

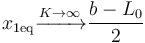
$x_{1\mathrm{eq}}\xrightarrow{K\to\infty} \frac{b-L_0}{2}$

que nos dice que la masa se queda a una distancia

L 0 / 2

del centro y por tanto el muelle central tiene una longitud fijada igual a

L 0

.

2.3 Ecuaciones para las elongaciones

Definimos ahora las elongaciones como las diferencias respecto a las posiciones de equilibrio

$x_1= x_{1\mathrm{eq}} + s_1\qquad\qquad x_2= x_{2\mathrm{eq}} + s_2$

En términos de las elongaciones las ecuaciones de movimiento quedan en la forma

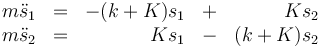
$\begin{array}{rcrcr} m\ddot{s}_1 & = & -(k+K)s_1& + &K s_2\\ m\ddot{s}_2 & = & K s_1 & - & (k+K)s_2 \end{array}$

2.3.1 Solución artesanal

Este sistema de ecuaciones diferenciales puede resolverse de forma sencilla por simple manipulación de las ecuaciones. Sin embargo, esta técnica no es fácil de extender al caso general, por lo que luego daremos un procedimiento más sistemático.

Si sumamos las dos ecuaciones (lo que equivale a averiguar el movimiento del CM) nos queda

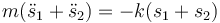
$m(\ddot{s}_1+\ddot{s}_2)=-k(s_1+s_2)$

que es la ecuación de un oscilador armónico de frecuencia 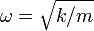$\omega = \sqrt{k/m}$ con solución

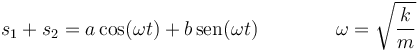
$s_1+s_2 = a \cos(\omega t) + b\,\mathrm{sen}(\omega t)\qquad \qquad\omega = \sqrt{\frac{k}{m}}$

Esto nos dice que el CM del sistema oscila con la frecuencia correspondiente a los resortes exteriores (de constante k), lo cual es lógico, pues el resorte interior ejerce una fuerza interna que no afecta a la posición del CM.

Si en lugar de sumar, restamos nos queda

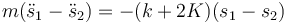
$m(\ddot{s}_1-\ddot{s}_2)= -(k+2K)(s_1-s_2)$

que es también la ecuación de un oscilador armónico, pero con una frecuencia diferente.

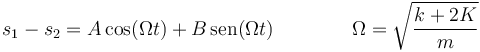
$s_1-s_2 = A \cos(\Omega t) + B\,\mathrm{sen}(\Omega t)\qquad \qquad\Omega = \sqrt{\frac{k+2K}{m}}$

El valor de la elongación de cada masa será una combinación de estas dos oscilaciones

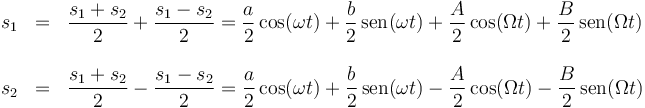
$\begin{array}{rcl} s_1&=&\dfrac{s_1+s_2}{2}+\dfrac{s_1-s_2}{2}=\dfrac{a}{2} \cos(\omega t) + \dfrac{b}{2}\,\mathrm{sen}(\omega t)+\dfrac{A}{2} \cos(\Omega t) + \dfrac{B}{2}\,\mathrm{sen}(\Omega t) \\ && \\ s_2&=&\dfrac{s_1+s_2}{2}-\dfrac{s_1-s_2}{2}=\dfrac{a}{2} \cos(\omega t) + \dfrac{b}{2}\,\mathrm{sen}(\omega t)-\dfrac{A}{2} \cos(\Omega t) - \dfrac{B}{2}\,\mathrm{sen}(\Omega t) \end{array}$

Como solución particular consideremos el caso de una respuesta impulsiva en la que a la masa 1 se le comunica una velocidad inicial $v 0$ estando en la posición de equilibrio, mientras que la 2 se encuentra inicialmente en reposo en su posición de equilibrio.

Imponiendo las condiciones iniciales

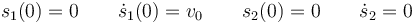
$s_1(0) = 0\qquad \dot{s}_1(0)=v_0\qquad s_2(0)=0\qquad\dot{s}_2=0$

resultan los coeficientes

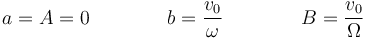
$a=A=0\qquad\qquad b = \frac{v_0}{\omega}\qquad\qquad B = \frac{v_0}{\Omega}$

y las elongaciones

$s_1=\frac{v_0}{2}\left(\frac{\mathrm{sen}(\omega t)}{\omega}+\frac{\mathrm{sen}(\Omega t)}{\Omega}\right)\qquad\qquad s_2=\frac{v_0}{2}\left(\frac{\mathrm{sen}(\omega t)}{\omega}-\frac{\mathrm{sen}(\Omega t)}{\Omega}\right)$

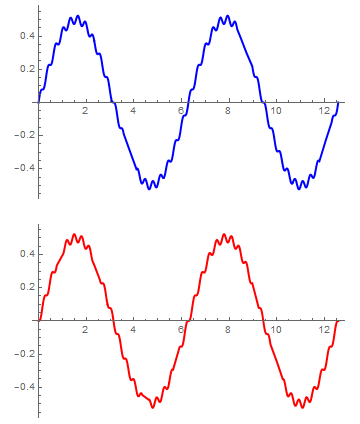
Así tomando unas unidades tales que $v 0 = 1$ $ω = 1$ y $Ω = 2ω$ queda

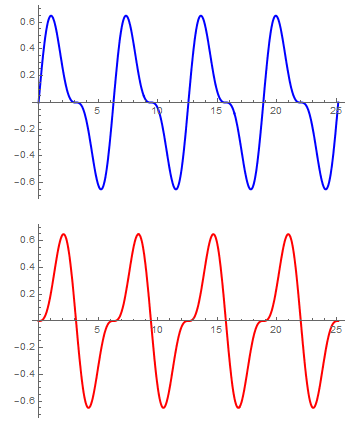
mientras que si tomamos un valor de K pequeño, de forma que $Ω = 1.1ω$

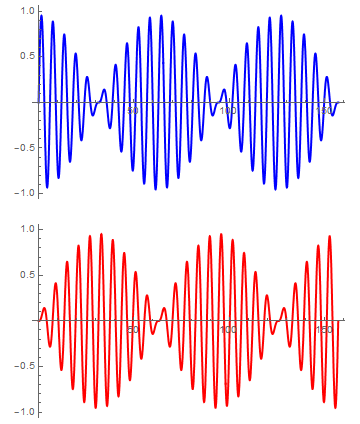
Para un valor de K grande (muelle central muy rígido) podemos hacer $Ω = 20ω$ , por ejemplo

2.3.2 Solución sistemática

El método anterior vale si a simple vista podemos determinar una combinación lineal de las variables de forma que en el primer miembro y en el segundo aparezca la misma combinación, pero eso no siempre es evidente. Por ello, conviene sistematizar el método.

La base es admitir que las soluciones particulares van a ser oscilantes, ambas con la misma frecuencia y por tanto se pueden escribir en términos de amplitudes complejas

$s_1=\hat{s}_1 \mathrm{e}^{\mathrm{j}\omega t}\qquad\qquad s_2=\hat{s}_2 \mathrm{e}^{\mathrm{j}\omega t}$

donde aquí $ω$ es una frecuencia desconocida por ahora. La solución general será una combinación lineal de las diferentes soluciones posibles.

Si sustituimos estas soluciones en las ecuaciones de movimiento nos queda

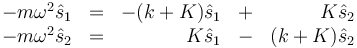
$\begin{array}{rcrcr} -m\omega^2\hat{s}_1 & = & -(k+K)\hat{s}_1& + &K \hat{s}_2\\ -m\omega^2\hat{s}_2 & = & K \hat{s}_1 & - & (k+K)\hat{s}_2 \end{array}$

Agrupando términos

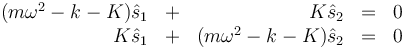
$\begin{array}{rcrcr} (m\omega^2-k-K)\hat{s}_1 & + & K \hat{s}_2 & = & 0\\ K \hat{s}_1 & + & (m\omega^2-k-K)\hat{s}_2 & = &0 \end{array}$

Esto es un sistema de dos ecuaciones con dos incógnitas pero homogéneo. Para que tenga solución no trivial el determinante de los coeficientes debe anularse

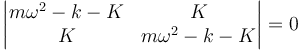
$\left|\begin{matrix} m\omega^2-k-K & K \\ K & m\omega^2-k-K\end{matrix}\right| = 0$

lo cual conduce a la ecuación

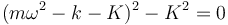
$(m\omega^2-k-K)^2 - K^2 = 0\,$

Si desarrollamos, nos dará una ecuación de cuarto grado que en realidad es una ecuacion de segundo grado en $ω 2$ . las soluciones serán dos pares de soluciones que nos dan las frecuencias de oscilación posible.

En este caso, podemos resolver sin necesidad de desarrollar

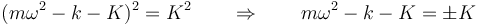
$(m\omega^2-k-K)^2 = K^2 \qquad\Rightarrow\qquad m\omega^2-k-K = \pm K$

Despejamos la frecuencia al cuadrado

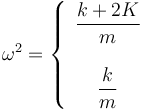
$\omega^2 = \left\{\begin{array}{c}\dfrac{k+2K}{m} \\ \\ \dfrac{k}{m}\end{array}\right.$

Para cada valor de la frecuencia al cuadrado habrá unos valores para los coeficientes. Tomando una cualquiera de las dos ecuaciones resulta

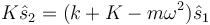
$K\hat{s}_2 =(k+K-m\omega^2)\hat{s}_1$

Cuando $ω 2 = k / m$ nos da 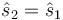$\hat{s}_2=\hat{s}_1$ y cuando $ω 2 = (k + 2 K) / m$ resulta 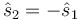$\hat{s}_2=-\hat{s}_1$ . Puesto que la solución sompleta es una combinación lineal de las funciones base, podemos escribir ésta como

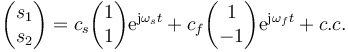
$\begin{pmatrix}s_1 \\ s_2\end{pmatrix}=c_s\begin{pmatrix}1 \\ 1\end{pmatrix}\mathrm{e}^{\mathrm{j}\omega_s t} + c_f\begin{pmatrix}1 \\ -1\end{pmatrix}\mathrm{e}^{\mathrm{j}\omega_f t}+c.c.$

donde “c.c.” significa complejo conjugado (ya que la solución debe ser real) y los subíndices s y f representan lento y rápido (en inglés), ya que la menor frecuencia implica oscilaciones más lentas y la mayor oscilaciones más rápidas.

Matemáticamente, lo que hemos hecho es calculas los autovectores y autovalores de la matriz y expresar la solución como combinación de los autovectores.

Cada una de estas soluciones base se denomina un modo normal de vibración y la solución completa es una combinación de los modos normales.

En este caso concreto, los dos modos poseen interpretación sencilla.

El modo lento, de frecuencia 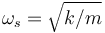$\omega_s =\sqrt{k/m}$ es un modo antisimétrico en el que cuando una masa se mueve hacia el centro del sistema la otra se aleja de él.
El modo rápido, de frecuencia 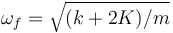$\omega_f = \sqrt{(k+2K)/m}$ es un modo simétrico, en el que las dos masas se acercan o s alejan del centro simultáneamente.

3 Caso general de dos osciladores

A partir del caso simétrico anterior puede generalizarse a un sistema de dos osciladores más general.

La idea es que las ecuaciones de movimiento para las elongaciones, una vez calculadas las posiciones de equilibrio, se pueden poner en la forma

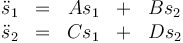
$\begin{array}{rcrcl} \ddot{s}_1 & = & A s_1 & + & B s_2 \\ \ddot{s}_2 & = & C s_1 & + & D s_2\end{array}$

Así, por ejemplo, para el problema con el que iniciamos este artículo tenemos las ecuaciones de movimiento

$m_1\ddot{s}_1 = -k_1 s_1 + k_2(s_2-s_1) \qquad\qquad m_2\ddot{s}_2 = -k_2(s_2-s_1)$

que nos dan los coeficientes

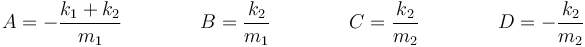
$A=-\frac{k_1+k_2}{m_1}\qquad\qquad B= \frac{k_2}{m_1}\qquad\qquad C=\frac{k_2}{m_2}\qquad\qquad D = -\frac{k_2}{m_2}$

Entonces, suponiendo soluciones armónicas llegamos a que debe anularse el determinante

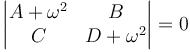
$\left| \begin{matrix} A+\omega^2 & B \\ C & D+\omega^2\end{matrix}\right|=0$

que produce una ecuación de segundo grado en $ω 2$

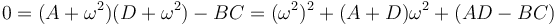
$0=(A+\omega^2)(D+\omega^2)- BC = (\omega^2)^2+(A+D)\omega^2 + (AD-BC)\,$

cuya solución nos da las dos frecuencias. Una vez que las tenemos calculamos las relaciones entre los coeficientes y escribimos la solución general como una combinación de estos modos normales.

4 El caso con rozamiento

Si los resortes tienen rozamiento viscoso, podemos generalizar el método anterior incluyendo nuevos términos en las ecuaciones.

Volviendo al ejemplo simétrico, supongamos que los muelles exteriores tienen una constante de amortiguamiento $γ$ y el resorte central una constante $Γ$ . En ese caso, las posiciones de equilibrio no cambian y las ecuaciones de movimiento para las elongaciones quedan en la forma

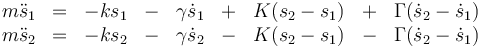
$\begin{array}{rcrcrcrcl} m\ddot{s}_1 & = & -ks_1& -&\gamma\dot{s}_1& + &K (s_2-s_1) & + &\Gamma(\dot{s}_2-\dot{s}_1)\\ m\ddot{s}_2 & = & -ks_2& -&\gamma\dot{s}_2& - &K (s_2-s_1) & - &\Gamma(\dot{s}_2-\dot{s}_1)\\ \end{array}$

o, agrupando términos,

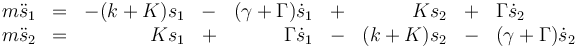
$\begin{array}{rcrcrcrcl} m\ddot{s}_1 & = & -(k+K)s_1& -&(\gamma+\Gamma)\dot{s}_1& + &K s_2 & + &\Gamma \dot{s}_2\\ m\ddot{s}_2 & = & Ks_1& +&\Gamma\dot{s}_1& - &(k+K) s_2 & - &(\gamma+\Gamma)\dot{s}_2\\ \end{array}$

Vemos que la diferencia con el caso sin rozamiento es la aparición de términos proporcionales a las velocidades.

4.1 Solución artesanal

De nuevo podemos resolver este problema sumando y restando las ecuaciones. Si las sumamos queda

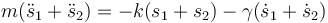
$m(\ddot{s}_1+\ddot{s}_2)=-k(s_1+s_2)-\gamma(\dot{s}_1+\dot{s}_2)$

que es la ecuación de un oscilador armónico amortiguado con frecuencia propia y factor de amortiguamiento

$\omega_0=\sqrt{\frac{k}{m}}\qquad\qquad \beta = \frac{\gamma}{2m}$

Si en lugar de sumar restamos nos da

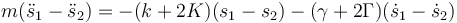
$m(\ddot{s}_1-\ddot{s}_2)=-(k+2K)(s_1-s_2)-(\gamma+2\Gamma)(\dot{s}_1-\dot{s}_2)$

que es de nuevo la ecuación de un oscilador amortiguado de constantes

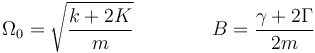
$\Omega_0=\sqrt{\frac{k+2K}{m}}\qquad\qquad B=\frac{\gamma+2\Gamma}{2m}$

Entonces, podemos tener diferntes casos, según los valores de los parámetros:

Que los dos osciladores sean subamortiguados
Que uno sea subamortiguado y el otro sobreamortiguado
Que los dos sean sobreamortiguados

Esto da una amplia variedad de soluciones aunque todas serán combinaciones de exponenciales decrecientes.

4.2 Solución sistemática

El procedimiento general es el mismo que para el caso sin rozamiento, suponemos soluciones oscilantes

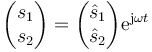
$\begin{pmatrix} s_1 \\ s_2 \end{pmatrix} = \begin{pmatrix} \hat{s}_1 \\ \hat{s}_2 \end{pmatrix} \mathrm{e}^{\mathrm{j}\omega t}$

aunque ahora $ω$ será una cantidad compleja. Llevando esta solución al sistema de ecuaciones de movimiento obtenemos el sistema

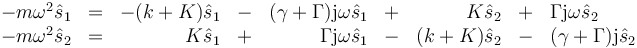
$\begin{array}{rcrcrcrcl} -m\omega^2\hat{s}_1 & = & -(k+K)\hat{s}_1& -&(\gamma+\Gamma)\mathrm{j}\omega\hat{s}_1& + &K \hat{s}_2 & + &\Gamma\mathrm{j}\omega\hat{s}_2\\ -m\omega^2\hat{s}_2 & = & K\hat{s}_1& +&\Gamma\mathrm{j}\omega\hat{s}_1& - &(k+K) \hat{s}_2 & - &(\gamma+\Gamma)\mathrm{j}\hat{s}_2\\ \end{array}$

y, agrupando términos

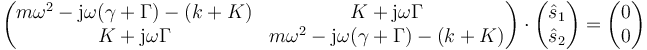
$\begin{pmatrix}m\omega^2-\mathrm{j}\omega(\gamma+\Gamma)-(k+K) & K+\mathrm{j}\omega\Gamma \\ K+\mathrm{j}\omega\Gamma & m\omega^2-\mathrm{j}\omega(\gamma+\Gamma)-(k+K)\end{pmatrix}\cdot\begin{pmatrix}\hat{s}_1 \\ \hat{s}_2\end{pmatrix}=\begin{pmatrix}0 \\ 0\end{pmatrix}$

De nuevo, para que este sistema tenga solución, debe anularse el determinante. El resultado en el caso con rozamiento es una ecuación de cuarto grado en el que las cuatro raíces son complejas y distintas. La solución general del problema será una combinación lineal de las cuatro soluciones.

5 Oscilaciones forzadas

Si suponemos un sistema de osciladires acoplados amortiguados sometidos a una fuerza oscilante

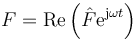
$F = \mathrm{Re}\left(\hat{F}\mathrm{e}^{\mathrm{j}\omega t}\right)$

el tratamiento es similar al caso de un solo oscilador, pero resolviendo ahora un sistema de ecuaciones algebraicas para las diferentes amplitudes.

Cuando realizamos la gráfica de la amplitud de las oscilaciones como función de la frecuencia de la fuerza aplicada obtenemos varios picos, correspondientes a las diferentes frecuencias propias. Cuando aplicamos una fuerza oscilante podemos excitar un modo u otro, dependiendo de la frecuencia de la excitación.

Oscilaciones acopladas (CMR)

De Laplace

Contenido

1 Introducción

2 Sistema simétrico

2.1 Ecuaciones de movimiento

2.2 Posición de equilibrio

2.3 Ecuaciones para las elongaciones

2.3.1 Solución artesanal

2.3.2 Solución sistemática

3 Caso general de dos osciladores

4 El caso con rozamiento

4.1 Solución artesanal

4.2 Solución sistemática

5 Oscilaciones forzadas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES