No Boletín - Diagonales de un rombo
De Laplace
1 Enunciado
Demuestre que las diagonales de un rombo son perpendiculares entre sí.
2 Solución
Sean ABCD los vértices del rombo. Se verifica que, por ser un paralelogramo

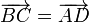
y por sus lados de la misma longitud

Las diagonales del rombo vienen dadas por los vectores
 y
y 
Multiplicando escalarmente estos dos vectores
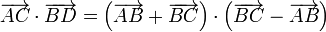
Desarrollando la suma por diferencia

y, por la igualdad entre las longitudes de los lados
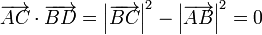
Por tanto, las diagonales son ortogonales.






