No Boletín - Trabajo y fuerza en un movimiento armónico simple (Ex.Ene/13)
De Laplace
1 Enunciado
Sea una partícula, de masa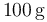 
, que describe un movimiento armónico simple cuya ecuación horaria es:
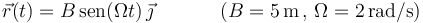
- ¿Cuánto vale el trabajo realizado sobre la partícula en el trayecto desde
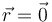hasta 
?
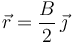- ¿Cuál es el valor de la fuerza que actúa sobre la partícula cuando ésta se halla en la posición
?
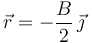2 Solución
Derivando el vector de posición de la partícula respecto al tiempo una y dos veces, obtenemos su velocidad y su aceleración, respectivamente:
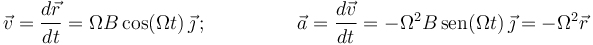
Y, conforme a la segunda ley de Newton, la fuerza que actúa sobre la partícula es:
siendo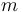 
la masa de la partícula.
Para determinar el valor de la fuerza que actúa sobre la partícula cuando ésta se halla en la posición 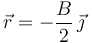, basta sustituir en la fórmula anterior ese valor concreto de 
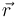, así como los valores numéricos 
, 
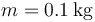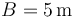y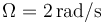 
:
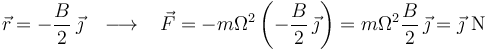
Para calcular el trabajo realizado sobre la partícula en el trayecto desde 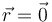hasta 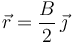, determinamos primero la celeridad de la partícula al inicio (
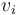) y al final (
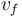) de dicho trayecto:
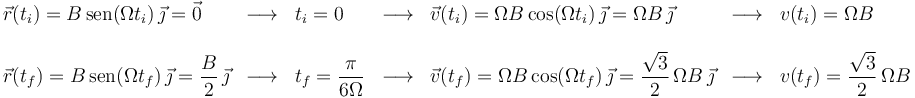
y, finalmente, aplicamos el teorema de las fuerzas vivas (trabajo igual a variación de energía cinética):
![W_{t_i}^{t_f}=K(t_f)-K(t_i)=\frac{1}{2}m\left[v^2(t_f)-v^2(t_i)\right]=\frac{1}{2}\,m\,\Omega^2B^2\left[\displaystyle\frac{3}{4}-1\right]=-\frac{1}{8}\,m\,\Omega^2B^2=-1.25\,\mathrm{J}](/wiki/images/math/c/d/c/cdc8a3311fd345f050f2255dd144c887.png)
