No Boletín - Tercera ley de Kepler (Ex.Nov/12)
De Laplace
1 Enunciado
El período 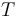 de revolución de un planeta alrededor del Sol se puede calcular mediante el siguiente producto de
potencias:
de revolución de un planeta alrededor del Sol se puede calcular mediante el siguiente producto de
potencias:
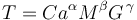
donde 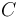 es un factor adimensional,
es un factor adimensional,  es la longitud del semieje mayor de la órbita elíptica del planeta,
es la longitud del semieje mayor de la órbita elíptica del planeta, 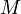 es la masa del Sol, y
es la masa del Sol, y 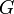 es la constante de gravitación universal (la cual se mide en
N
es la constante de gravitación universal (la cual se mide en
N m2/kg2 en el SI). Utilice el análisis dimensional para responder a la siguiente pregunta: ¿cuáles son los valores correctos de los exponentes
m2/kg2 en el SI). Utilice el análisis dimensional para responder a la siguiente pregunta: ¿cuáles son los valores correctos de los exponentes 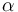 ,
, 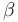 y
y 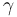 ?
?
2 Solución
La ecuación dada en el enunciado ha de ser dimensionalmente homogénea. Por tanto, los valores de los exponentes 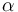 ,
, 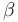 y
y 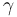 no pueden ser cualesquiera, sino precisamente los compatibles con dicha condición de homogeneidad dimensional.
no pueden ser cualesquiera, sino precisamente los compatibles con dicha condición de homogeneidad dimensional.
De las magnitudes físicas presentes en la citada ecuación, la única cuyas dimensiones no son obvias es la constante de gravitación universal. Por eso se nos facilita su unidad en el SI, para que podamos deducir su ecuación dimensional:
![\mathrm{unidad}\,\,\mathrm{SI}\,\,\mathrm{de}\,\, G = 1\,\mathrm{N}\cdot\mathrm{m}^2\mathrm{/kg}^2\,\,\,\,\,\, \Longrightarrow \,\,\,\,\,\,[G\,]=\frac{MLT^{-2}L^2}{M^2}=M^{-1}L^3T^{-2}](/wiki/images/math/4/a/3/4a38b7b4b57d24de936bfca150d81a89.png)
Ya estamos preparados para tomar dimensiones en la ecuación del período de revolución dada en el enunciado. Al hacerlo, desaparece 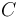 por ser un factor adimensional, y se obtiene:
por ser un factor adimensional, y se obtiene:
![[T]=[a]^{\alpha}[M]^{\beta}[G\,]^{\,\gamma} \,\,\,\,\,\Longrightarrow\,\,\,\,\,T = L^{\alpha}M^{\beta}\left(M^{-1}L^3T^{-2}\right)^{\gamma}\,\,\,\,\,\Longrightarrow\,\,\,\,\, T = M^{\beta-\gamma}L^{\alpha+3\gamma}T^{-2\gamma}\,](/wiki/images/math/e/6/5/e65a4e1dfdd9e65887c005898fb2b93b.png)
Igualando entre sí los exponentes de cada magnitud básica en ambos miembros (obviamente la ausencia de una magnitud equivale a un exponente nulo), obtenemos:
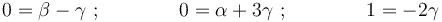
de donde: