No Boletín - Punto de aceleración nula (Ex.Feb/17)

De Laplace

1 Enunciado

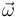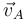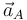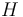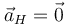Considérese un sólido rígido que realiza un movimiento plano arbitrario pero con una velocidad angular $\vec{\omega}\,$ constante en el tiempo y no nula. Sea $A\,$ un punto cualquiera del sólido en el plano director (con velocidad $\vec{v}_{A}\,$ y aceleración $\vec{a}_{A}\,$ ). Entonces, se puede comprobar que dicho sólido tiene en el plano director un punto $H\,$ cuya aceleración es nula ( $\vec{a}_{H}=\vec{0}\,$ ).

Determine el vector 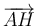$\overrightarrow{AH}\,$ que define la posición del punto de aceleración nula respecto al punto $A\,$ .

2 Solución

Utilizando la ecuación del campo de aceleraciones de un sólido rígido en movimiento plano (forma simplificada) para relacionar las aceleraciones de los puntos 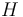$H\,$ y $A\,$ , se tiene que:

$\vec{a}_H=\vec{a}_A+\vec{\alpha}\times\overrightarrow{AH}-|\,\vec{\omega}\,|^2\overrightarrow{AH}$

Y como, atendiendo al enunciado del ejercicio, se sabe que:

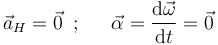
$\vec{a}_H=\vec{0}\,\,\,;\,\,\,\,\,\,\,\,\,\vec{\alpha}=\frac{\mathrm{d}\vec{\omega}}{\mathrm{d}t}=\vec{0}$

se llega a:

$\vec{0}=\vec{a}_A-|\,\vec{\omega}\,|^2\overrightarrow{AH}\,\,\,\,\,\,\,\,\,\longrightarrow\,\,\,\,\,\,\,\,\,\overrightarrow{AH}=\frac{\vec{a}_A}{|\,\vec{\omega}\,|^2}$

No Boletín - Punto de aceleración nula (Ex.Feb/17)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES