Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Placa cuadrada que empuja a un disco (Ex.Sep/14)

De Laplace

Contenido

1 Enunciado

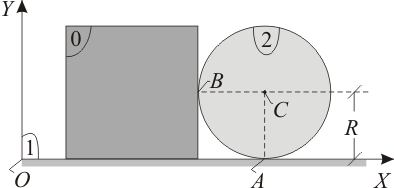
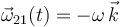El sistema de la figura está constituido por tres sólidos rígidos: la escuadra fija OXY\, (sólido "1"); una placa cuadrada (sólido "0") que se traslada con velocidad constante \vec{v}^{\,\mathrm{tras}}_{01}(t)=v_0\,\vec{\imath}\, y cuyo lado inferior está completamente en contacto con el eje OX\,; y un disco (sólido "2"), de centro C\, y radio R\,, que rota con velocidad angular constante \vec{\omega}_{21}(t)=-\omega\,\vec{k}\,, y que en todo instante mantiene contacto puntual con el eje OX\, (punto A\,) y con la placa cuadrada que lo empuja (punto B\,).

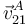  1. ¿Cuánto vale la velocidad instantánea \vec{v}^{A}_{21}\,\,?
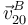  2. ¿Y la velocidad instantánea \vec{v}^{B}_{20}\,\,?
  3. ¿Dónde se halla situado el centro instantáneo de rotación I_{20}\,\,?

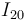2 Velocidad instantánea del punto A en el movimiento {21}

Dado que la placa cuadrada se traslada con velocidad constante \vec{v}^{\,\mathrm{tras}}_{01}(t)=v_0\,\vec{\imath}\, y el disco se mantiene siempre en contacto puntual con ella y con el eje OX\,, es evidente que el centro C\, del disco realizará un movimiento rectilíneo y uniforme con esa misma velocidad:

\vec{v}^{\, C}_{21}(t)=v_0\,\vec{\imath}

Como también conocemos la velocidad angular del disco 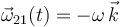\vec{\omega}_{21}(t)=-\omega\,\vec{k}\,, podemos determinar la velocidad instantánea 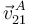\vec{v}^{\, A}_{21}\, aplicando la ecuación del campo de velocidades correspondiente:

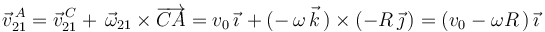
\vec{v}^{\, A}_{21}=\vec{v}^{\, C}_{21}+\,\vec{\omega}_{21}\times\overrightarrow{CA}=v_0\,\vec{\imath}\,+(-\,\omega\,\vec{k}\,)\times(-R\,\vec{\jmath}\,)=(v_0-\omega R\,)\,\vec{\imath}

El hecho de que 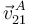\vec{v}^{\, A}_{21}\, sea no nula (si 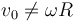v_0\neq\omega R\,) significa que existe deslizamiento entre el disco y el eje OX\,.

3 Velocidad instantánea del punto B en el movimiento {20}

Aplicando otra vez la ecuación del campo de velocidades del movimiento {21}, podemos obtener la velocidad instantánea 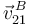\vec{v}^{\, B}_{21}\,:

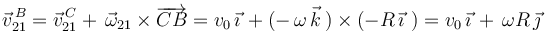
\vec{v}^{\, B}_{21}=\vec{v}^{\, C}_{21}+\,\vec{\omega}_{21}\times\overrightarrow{CB}=v_0\,\vec{\imath}\,+(-\,\omega\,\vec{k}\,)\times(-R\,\vec{\imath}\,\,)=v_0\,\vec{\imath}\,+\,\omega R\,\vec{\jmath}

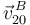Y aplicando la ley de composición de velocidades en el punto B\,, determinamos la velocidad instantánea \vec{v}^{\, B}_{20}\,:

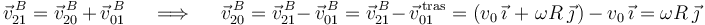
\vec{v}^{\, B}_{21}=\vec{v}^{\, B}_{20}\,+\,\vec{v}^{\, B}_{01}\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\vec{v}^{\, B}_{20}=\vec{v}^{\, B}_{21}-\,\vec{v}^{\, B}_{01}=\vec{v}^{\, B}_{21}-\,\vec{v}^{\,\mathrm{tras}}_{01}=(v_0\,\vec{\imath}\,\,+\,\,\omega R\,\vec{\jmath}\,)\,-\,v_0\,\vec{\imath}=\omega R\,\vec{\jmath}

El hecho de que 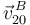\vec{v}^{\, B}_{20}\, no sea nula significa que existe deslizamiento entre el disco y la placa cuadrada.

4 Centro instantáneo de rotación del movimiento {20}

Para determinar la posición del centro instantáneo de rotación 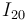I_{20}\,, podemos aplicar el procedimiento analítico.

La ley de composición de velocidades angulares nos permite calcular la velocidad angular del movimiento {20}:

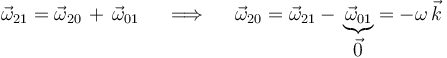
\vec{\omega}_{21}=\vec{\omega}_{20}\,+\,\vec{\omega}_{01}\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\vec{\omega}_{20}=\vec{\omega}_{21}-\,\underbrace{\vec{\omega}_{01}}_{\displaystyle\vec{0}}=-\omega\,\vec{k}

donde se ha tenido en cuenta que el movimiento {01} es una traslación y, por tanto, la velocidad angular 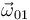\vec{\omega}_{01}\, es nula.

Entonces, la posición del centro instantáneo de rotación 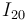I_{20}\, respecto al punto B\, se determina mediante la fórmula deducida en la teoría:

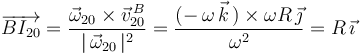
\overrightarrow{BI_{20}}=\frac{\vec{\omega}_{20}\times\vec{v}^{\, B}_{20}}{|\,\vec{\omega}_{20}\,|^{2}}=\frac{(-\,\omega\,\vec{k}\,)\times\omega R\,\vec{\jmath}}{\omega^2}=R\,\vec{\imath}

Pero a una distancia R\, a la derecha del punto B\, se encuentra el centro C\, del disco. Por tanto, concluimos que:

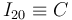
I_{20}\equiv C

A la misma conclusión se llega calculando la velocidad del punto C\, en el movimiento {20} mediante la ley de composición de velocidades:

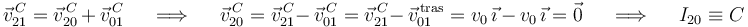
\vec{v}^{\, C}_{21}=\vec{v}^{\, C}_{20}\,+\,\vec{v}^{\, C}_{01}\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\vec{v}^{\, C}_{20}=\vec{v}^{\, C}_{21}-\,\vec{v}^{\, C}_{01}=\vec{v}^{\, C}_{21}-\,\vec{v}^{\,\mathrm{tras}}_{01}=v_0\,\vec{\imath}\,-\,v_0\,\vec{\imath}=\vec{0}\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,I_{20}\equiv C

En realidad, el centro C\, del disco mantiene una posición constante respecto a la placa cuadrada y, por tanto, es un punto fijo o centro permanente de rotación en el movimiento {20}.

Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Placa_cuadrada_que_empuja_a_un_disco_(Ex.Sep/14)"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 21:32, 20 mar 2015. - Esta página ha sido visitada 4.600 veces. - Aviso legal - Acerca de Laplace