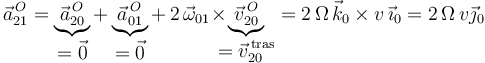No Boletín - Placa cuadrada deslizando sobre escuadra giratoria (Ex.Ene/18)

De Laplace

1 Enunciado

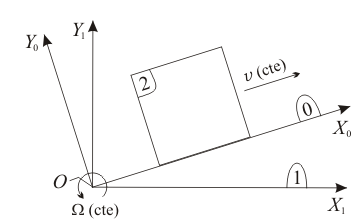
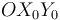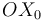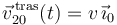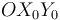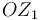Una placa cuadrada (sólido "2"), contenida en el plano $OX_0Y_0\,$ , desliza sobre el eje $OX_0\,$ (sólido "0") con velocidad relativa constante $\vec{v}^{\,\mathrm{tras}}_{20}(t)=v\,\vec{\imath}_0\,$ . 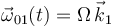Al mismo tiempo, la escuadra $OX_0Y_0\,$ (sólido "0"), articulada en el punto $O\,$ a la escuadra fija y coplanaria $OX_1Y_1\,$ (sólido "1"), rota alrededor del eje fijo $OZ_1\,$ con velocidad angular constante $\vec{\omega}_{01}(t)=\Omega\,\vec{k}_1\,$ .

Determine el vector de posición del C.I.R. del movimiento $\{21\}\,$ .
Determine la aceleración del punto $O\,$ en el movimiento $\{21\}\,$ .

2 Determinación analítica de la posición del C.I.R.{21}

Determinamos primero la velocidad angular 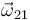$\vec{\omega}_{21}\,$ mediante la ley de composición de velocidades angulares:

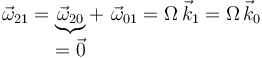
$\vec{\omega}_{21}=\underbrace{\vec{\omega}_{20}}_{\displaystyle =\vec{0}}+\,\,\vec{\omega}_{01}=\Omega\,\vec{k}_1=\Omega\,\vec{k}_0$

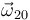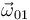donde se ha tenido en cuenta que $\vec{\omega}_{20}\,$ es nula por ser el movimiento $\{20\}\,$ una traslación, y que $\vec{\omega}_{01}\,$ es un dato del ejercicio.

A continuación, determinamos la velocidad 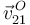$\vec{v}^{\, O}_{21}\,$ mediante la ley de composición de velocidades:

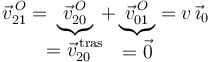
$\vec{v}^{\, O}_{21}=\!\!\underbrace{\vec{v}^{\, O}_{20}}_{\displaystyle =\vec{v}^{\, \mathrm{tras}}_{20}}\!\!+\underbrace{\vec{v}^{\, O}_{01}}_{\displaystyle =\vec{0}}=v\,\vec{\imath}_0$

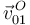donde se ha tenido en cuenta que el campo de velocidades del movimiento $\{20\}\,$ es uniforme (traslación) y de valor conocido (dato), y que $\vec{v}^{\, O}_{01}\,$ es nula por ser $O\,$ un punto fijo en el movimiento $\{01\}\,$ .

Sustituyendo el valor de estas magnitudes en la fórmula deducida en la teoría, se obtiene el vector de posición del C.I.R.{21}:

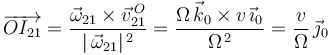
$\overrightarrow{OI_{21}}=\frac{\vec{\omega}_{21}\times\vec{v}^{\, O}_{21}}{|\,\vec{\omega}_{21}|^{\, 2}}=\frac{\Omega\,\vec{k}_0\times v\,\vec{\imath}_0}{\Omega^{\, 2}}=\frac{v}{\Omega}\,\vec{\jmath}_0$

3 Aceleración del punto O en el movimiento {21}

Calculamos primero la aceleración 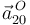$\vec{a}^{\, O}_{20}\,$ a partir de su definición:

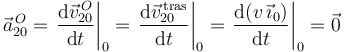
$\vec{a}^{\, O}_{20}=\left.\frac{\mathrm{d}\vec{v}^{\, O}_{20}}{\mathrm{d}t}\right|_{0}=\left.\frac{\mathrm{d}\vec{v}^{\, \mathrm{tras}}_{20}}{\mathrm{d}t}\right|_{0}=\left.\frac{\mathrm{d}(v\,\vec{\imath}_0)}{\mathrm{d}t}\right|_{0}=\vec{0}$

Por otra parte, la aceleración 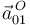$\vec{a}^{\, O}_{01}\,$ también es nula por ser $O\,$ un punto fijo en el movimiento $\{01\}\,$ :

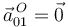
$\vec{a}^{\, O}_{01}=\vec{0}$

Por último, determinamos la aceleración 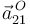$\vec{a}^{\, O}_{21}\,$ aplicando la ley de composición de aceleraciones:

$\vec{a}^{\, O}_{21}=\underbrace{\vec{a}^{\, O}_{20}}_{\displaystyle =\vec{0}}+\underbrace{\vec{a}^{\, O}_{01}}_{\displaystyle =\vec{0}}+\,2\,\vec{\omega}_{01}\!\times\!\!\!\!\underbrace{\vec{v}^{\, O}_{20}}_{\displaystyle =\vec{v}^{\, \mathrm{tras}}_{20}}=2\,\Omega\,\vec{k}_0\times v\,\vec{\imath}_0=2\,\Omega\, v\vec{\jmath}_0$

No Boletín - Placa cuadrada deslizando sobre escuadra giratoria (Ex.Ene/18)

De Laplace

1 Enunciado

2 Determinación analítica de la posición del C.I.R.{21}

3 Aceleración del punto O en el movimiento {21}

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES