No Boletín - Persecución en el eje OX (Ex.Oct/19)

De Laplace

Contenido

1 Enunciado
2 Cuestiones previas
3 Cinemática del coche y del motorista
4 Respuesta a las dos preguntas formuladas

1 Enunciado

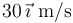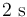Un coche circula por una carretera rectilínea (eje OX) con una velocidad constante de $30\,\vec{\imath}\,\,\mathrm{m/s}\,$ , y en cierto instante pasa por el lado de un motorista que se encuentra parado en el arcén. 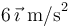Transcurrido un tiempo de $2\,\,\mathrm{s}\,$ desde que pasó por su lado, el motorista inicia la persecución del coche, que realiza del siguiente modo: partiendo del reposo, mantiene una aceleración constante de $6\,\vec{\imath}\,\,\mathrm{m/s}^2\,$ hasta el instante en el que alcanza una velocidad de 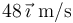$48\,\vec{\imath}\,\,\mathrm{m/s}\,$ , instante a partir del cual mantiene constante dicha velocidad.

¿Cuánto tiempo transcurre desde el inicio de la persecución hasta que el motorista alcanza al coche?
¿Qué longitud total habrá recorrido el motorista cuando alcance al coche?

2 Cuestiones previas

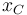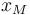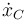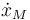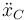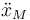Dado que el coche y el motorista realizan movimientos rectilíneos sobre el eje OX, prescindiremos del carácter vectorial de sus magnitudes cinemáticas. Por tanto, describiremos sus posiciones mediante las coordenadas $x_C\,$ y $x_M\,$ , sus velocidades mediante $\dot{x}_C\,$ y $\dot{x}_M\,$ , y sus aceleraciones mediante $\ddot{x}_C\,$ y $\ddot{x}_M\,$ .

Consideraremos que 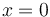$x=0\,\,$ es la posición en la cual el motorista se encuentra inicialmente parado, y que 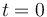$t=0\,\,$ es el instante en el cual el motorista inicia la persecución del coche.

Los instantes relevantes del problema son los siguientes:

$\begin{array}{lll} t=-2\,\,\mathrm{s} & \,\longrightarrow\,\,\, & \mathrm{el}\,\,\mathrm{coche}\,\,\mathrm{pasa}\,\,\mathrm{por}\,\,\mathrm{el}\,\,\mathrm{lado}\,\,\mathrm{del}\,\,\mathrm{motorista}\,\,\mathrm{en}\,\,\mathrm{la}\,\,\mathrm{posicion}\,\, x=0 \\ \\ t=0 & \,\longrightarrow\,\,\, & \mathrm{el}\,\,\mathrm{motorista}\,\,\mathrm{inicia}\,\,\mathrm{la}\,\,\mathrm{persecucion}\,\,\mathrm{del}\,\,\mathrm{coche} \,\,\mathrm{partiendo}\,\,\mathrm{del}\,\,\mathrm{reposo}\,\,\mathrm{en}\,\,\mathrm{la}\,\,\mathrm{posicion}\,\, x=0 \\ \\ t=t_1 & \,\longrightarrow\,\,\, & \mathrm{el}\,\,\mathrm{motorista}\,\,\mathrm{cambia}\,\,\mathrm{de}\,\,\mathrm{su}\,\,\mathrm{inicial}\,\,\,\mathrm{m.r.u.a.}\,\,\,\mathrm{a}\,\,\mathrm{un}\,\,\,\mathrm{m.r.u.}\,\,\mathrm{en}\,\,\mathrm{cierta}\,\,\mathrm{posicion}\,\, x=x_1 \\ \\ t=t_2 & \,\longrightarrow\,\,\, & \mathrm{el}\,\,\mathrm{motorista}\,\,\mathrm{alcanza}\,\,\mathrm{al}\,\,\mathrm{coche}\,\,\mathrm{en}\,\,\mathrm{cierta}\,\,\mathrm{posicion}\,\, x=x_2 \end{array}$

Conforme al enunciado, el coche realiza en todo instante un movimiento rectilíneo uniforme (m.r.u.), mientras que el motorista tiene una primera etapa (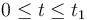 $0\leq t\leq t_1\,$ ) de movimiento rectilíneo uniformemente acelerado (m.r.u.a.) y una segunda etapa ( 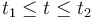$t_1\leq t\leq t_2\,$ ) de movimiento rectilíneo uniforme (m.r.u.).

Tanto el m.r.u. como el m.r.u.a. son movimientos elementales, y por ello utilizaremos sus ecuaciones sin necesidad de deducirlas. En general, son las siguientes:

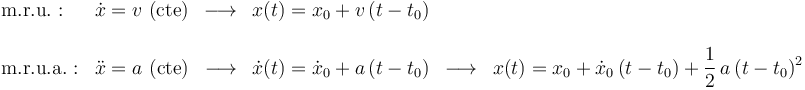
$\begin{array}{ll} \mathrm{m.r.u.}: & \dot{x}=v\,\,\mathrm{(cte)}\,\,\,\longrightarrow\,\,\, x(t)=x_0+v\,(t-t_0) \\ \\ \mathrm{m.r.u.a.}: & \ddot{x}=a\,\,\mathrm{(cte)} \,\,\,\longrightarrow\,\,\, \dot{x}(t)=\dot{x}_0+a\,(t-t_0)\,\,\,\longrightarrow\,\,\,x(t)=x_0+\dot{x}_0\,(t-t_0)+\displaystyle\frac{1}{2}\,a\,(t-t_0)^2 \end{array}$

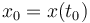donde $t_0\,$ es el instante inicial del movimiento, $x_0=x(t_0)\,$ es la posición inicial del móvil, y 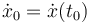$\dot{x}_0=\dot{x}(t_0)\,$ es su velocidad inicial.

3 Cinemática del coche y del motorista

La posición del coche queda definida en todo instante por la ecuación horaria:

$x_C(t)=30\,(t+2)\,\,\,\,\,\,\,\mathrm{(unidades}\,\,\mathrm{del}\,\,\mathrm{SI)}$

que corresponde a un m.r.u. con instante inicial 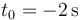$t_0=-2\,\mathrm{s}\,$ , posición inicial 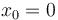$x_0=0\,\,$ y velocidad constante $v=30\,\mathrm{m/s}\,$ .

El movimiento del motorista en su primera etapa (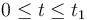 $0\leq t\leq t_1\,$ ) viene caracterizado por las ecuaciones:

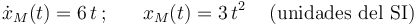
$\dot{x}_M(t)=6\,t\,;\,\,\,\,\,\,\,\,\,\, x_M(t)=3\,t^2\,\,\,\,\,\,\,\mathrm{(unidades}\,\,\mathrm{del}\,\,\mathrm{SI)}$

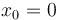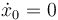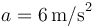que corresponden a un m.r.u.a. con instante inicial $t_0=0\,$ , posición inicial $x_0=0\,$ , velocidad inicial $\dot{x}_0=0\,$ (reposo inicial) y aceleración constante $a=6\,\mathrm{m/s}^2\,$ .

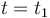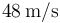Podemos entonces determinar el instante final $t=t_1\,$ de esta primera etapa del movimiento del motorista porque sabemos que termina cuando su velocidad es igual a $48\,\mathrm{m/s}\,$ :

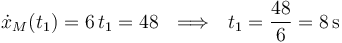
$\dot{x}_M(t_1)=6\,t_1=48\,\,\,\,\Longrightarrow\,\,\,\, t_1=\frac{48}{6}=8\,\mathrm{s}$

Entonces, la posición 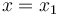$x=x_1\,$ del motorista al final de la primera etapa de su movimiento e inicio de la segunda etapa del mismo es:

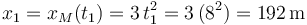
$x_1=x_M(t_1)=3\,t_1^2=3\,(8^2)=192\,\mathrm{m}$

En consecuencia, la posición del motorista durante la segunda etapa de su movimiento (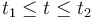 $t_1\leq t\leq t_2\,$ ) viene dada por la ecuación horaria:

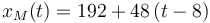
$x_M(t)=192+48\,(t-8)$

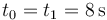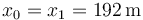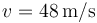que corresponde a un m.r.u. con instante inicial $t_0=t_1=8\,\mathrm{s}\,$ , posición inicial $x_0=x_1=192\,\mathrm{m}\,$ y velocidad constante $v=48\,\mathrm{m/s}\,$ .

4 Respuesta a las dos preguntas formuladas

Para poder determinar el instante en el cual el motorista alcanza al coche, necesitamos saber en qué etapa de su movimiento ocurre tal cosa. Si comparamos la posición ya calculada del motorista en el instante final de la primera etapa de su movimiento [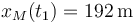 $x_M(t_1)=192\,\mathrm{m}\,$ ] con la posición del coche en dicho instante [ 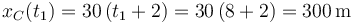$x_C(t_1)=30\,(t_1+2)=30\,(8+2)=300\,\mathrm{m}\,$ ] , comprobamos que aún no lo ha alcanzado y que, por tanto, lo hará durante la segunda etapa de su movimiento.

Así que, igualando las posiciones del motorista (segunda etapa de su movimiento) y del coche, determinamos el instante 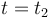$t=t_2\,\,$ en el cual el motorista alcanza al coche:

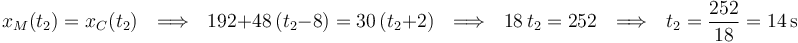
$x_M(t_2)=x_C(t_2) \,\,\,\,\Longrightarrow\,\,\,\, 192+48\,(t_2-8)=30\,(t_2+2) \,\,\,\,\Longrightarrow\,\,\,\, 18\,t_2=252 \,\,\,\,\Longrightarrow\,\,\,\, t_2=\frac{252}{18}=14\,\mathrm{s}$

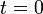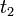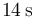Al haber considerado que la persecución se inició en $t=0\,$ , la respuesta a la primera pregunta del ejercicio coincide precisamente con $t_2\,$ . Por tanto, el tiempo transcurrido desde el inicio de la persecución hasta que el motorista alcanza al coche es de $14\,\mathrm{s}\,$ .

Finalmente, determinamos la posición 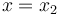$x=x_2\,$ del motorista en el instante 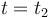$t=t_2\,$ en el cual da alcance al coche:

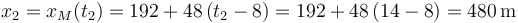
$x_2=x_M(t_2)=192+48\,(t_2-8)=192+48\,(14-8)=480\,\mathrm{m}$

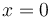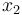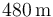Al haber considerado que $x=0\,\,\,$ corresponde a la posición en la cual el motorista se encontraba inicialmente parado, la respuesta a la segunda pregunta del ejercicio coincide precisamente con $x_2\,$ . Por tanto, la longitud total que habrá recorrido el motorista cuando alcance al coche es de $480\,\mathrm{m}\,$ .