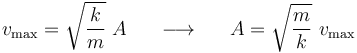No Boletín - Partícula unida a un muelle (Ex.Sep/14)

De Laplace

1 Enunciado

Una partícula de masa 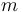$m\,$ se halla sujeta al extremo de un muelle cuyo otro extremo permanece fijo. El muelle tiene constante elástica 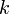$k\,$ y, bajo su acción exclusiva, la partícula realiza un movimiento armónico simple. ¿Qué relación existe entra la celeridad máxima 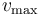$v_{\mathrm{max}}\,$ que alcanza la partícula durante el movimiento y la amplitud $A\,$ de su oscilación?

2 Solución

Definiendo el eje OX de tal modo que sea colineal con el movimiento rectilíneo de la partícula y que tenga su origen O en la posición de equilibrio de la misma, la segunda ley de Newton proyectada sobre dicho eje OX establecerá:

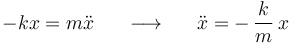
$-kx=m\ddot{x} \,\,\,\,\,\,\,\,\,\longrightarrow\,\,\,\,\,\,\,\,\, \ddot{x}=-\,\frac{k}{m}\,x$

ecuación diferencial que efectivamente reconocemos como la de un movimiento armónico simple de frecuencia angular $\sqrt{k/m}\,$ , y cuya solución sabemos que puede expresarse así:

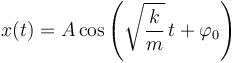
$x(t)=A\,\mathrm{cos}\left(\sqrt{\frac{k}{m}}\,t+\varphi_0\right)$

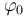donde $A\,$ y $\varphi_0\,$ son, respectivamente, la amplitud y la fase inicial del movimiento armónico simple.

Derivando respecto al tiempo la posición 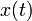$x(t)\,$ de la partícula y tomando valor absoluto, obtenemos su celeridad:

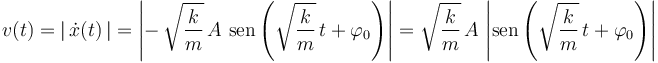
$v(t)=|\,\dot{x}(t)\,|=\left|-\,\sqrt{\frac{k}{m}}\,A\,\,\mathrm{sen}\left(\sqrt{\frac{k}{m}}\,t+\varphi_0\right)\right|=\sqrt{\frac{k}{m}}\,A\,\left|\mathrm{sen}\left(\sqrt{\frac{k}{m}}\,t+\varphi_0\right)\right|$

Y teniendo en cuenta que el valor máximo del valor absoluto del seno es la unidad, deducimos la relación existente entre la celeridad máxima 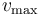$v_{\mathrm{max}}\,$ que alcanza la partícula durante el movimiento y la amplitud $A\,$ de su oscilación:

$v_{\mathrm{max}}=\sqrt{\frac{k}{m}}\,\,A \,\,\,\,\,\,\,\,\,\longrightarrow\,\,\,\,\,\,\,\,\, A=\sqrt{\frac{m}{k}}\,\,v_{\mathrm{max}}$

No Boletín - Partícula unida a un muelle (Ex.Sep/14)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES