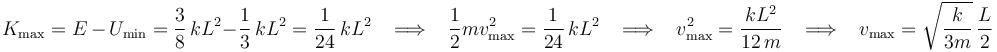No Boletín - Partícula unida a dos muelles (Ex.Feb/14)

De Laplace

1 Enunciado

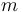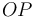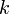Una partícula $P\,$ , de masa $m\,$ , se mueve en el eje $OX\,$ sometida exclusivamente a las fuerzas que ejercen sobre ella dos resortes elásticos ideales. Ambos resortes tienen longitud natural nula, pero uno de ellos ( $OP\,$ ) está anclado en el origen de coordenadas $O\,$ y tiene constante elástica $k\,$ , mientras que el otro ( 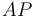$AP\,$ ) está anclado en el punto $A\,$ de coordenada 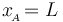$x_{_{\! A}}\!=L\,\,$ y tiene constante elástica $2k\,$ .

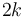¿Cuál es la posición de equilibrio?
¿Qué celeridad máxima alcanzará la partícula en su movimiento si en el instante inicial se halla en reposo en el punto medio entre $O\,$ y $A\,$ ?

2 Posición de equilibrio

La fuerza neta que actúa sobre la partícula $P\,$ es la suma vectorial de las fuerzas que ejercen sobre ella los dos resortes:

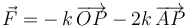
$\vec{F}=-\,k\,\overrightarrow{OP}-2k\,\overrightarrow{AP}$

y sustituyendo en esta expresión los vectores de posición de $P\,$ respecto a los puntos de anclaje de los resortes ( $O\,$ y $A\,$ ):

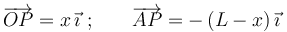
$\overrightarrow{OP}=x\,\vec{\imath}\,\,;\,\,\,\,\,\,\,\,\,\,\,\overrightarrow{AP}=-\,(L-x)\,\vec{\imath}$

se obtiene:

$\vec{F}=-\,k\,[x-2(L-x)]\,\vec{\imath}=k\,(2L-3x)\,\vec{\imath}$

Exigiendo la condición de equilibrio (fuerza neta igual a cero), obtenemos la posición de equilibrio de la partícula:

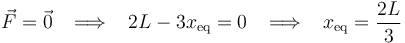
$\vec{F}=\vec{0}\,\,\,\,\,\Longrightarrow\,\,\,\,\,2L-3x_{\mathrm{eq}}=0\,\,\,\,\,\Longrightarrow\,\,\,\,\,x_{\mathrm{eq}}=\frac{2L}{3}$

3 Celeridad máxima

La energía cinética 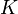$K\,$ de la partícula depende de su celeridad $v\,$ mediante la expresión:

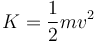
$K=\frac{1}{2}mv^2$

Las fuerzas ejercidas sobre la partícula por los resortes son conservativas, y como tales permiten que se les asocie una función energía potencial (elástica) que es función de la posición $x\,$ mediante la expresión:

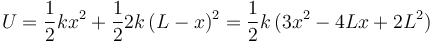
$U=\frac{1}{2}k x^2+\frac{1}{2}2k\,(L-x)^2=\frac{1}{2}k\,(3x^2-4Lx+2L^2)$

Dado que sobre la partícula no trabaja ninguna fuerza no conservativa, sabemos que su energía mecánica 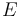$E\,$ (suma de su energía cinética y su energía potencial) permanece constante durante el movimiento:

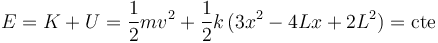
$E=K+U=\frac{1}{2}mv^2+\frac{1}{2}k\,(3x^2-4Lx+2L^2)=\mathrm{cte}$

Por el enunciado conocemos las condiciones iniciales del movimiento (reposo en el punto medio entre $O\,$ y $A\,$ ):

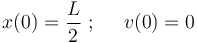
$x(0)=\frac{L}{2}\,\,;\,\,\,\,\,\,\,\, v(0)=0$

Así que la energía mecánica constante podemos evaluarla a partir de dichas condiciones iniciales:

$E=E(0)=\frac{1}{2}m[v(0)]^2+\frac{1}{2}k\,\left\{3[x(0)]^2-4L[x(0)]+2L^2\right\}=\frac{1}{2}k\left[3\left(\frac{L}{2}\right)^2-4L\left(\frac{L}{2}\right)+2L^2\right]=\frac{3}{8}\,kL^2$

Cuando la partícula alcance su celeridad máxima, también será máxima su energía cinética. Y teniendo en cuenta que la energía mecánica es constante, es obvio que la energía cinética máxima se alcanzará cuando la energía potencial sea mínima:

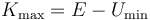
$K_{\mathrm{max}}=E-U_{\mathrm{min}}\,$

Pero sabemos que la energía potencial toma sus valores extremos (mínimos o máximos) en los puntos de equilibrio (en los cuales se anula la derivada primera de la función energía potencial respecto a su variable $x\,$ ). 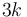En el caso que nos ocupa, ya hemos calculado la única posición de equilibrio de la partícula, y analizando la derivada segunda de la función energía potencial respecto a $x\,$ descubrimos que es positiva (su valor es constante e igual a $3k\,$ ) y que, por tanto, el punto de equilibrio corresponde a un mínimo de energía potencial. Así que:

$U_{\mathrm{min}}=U|_{x=x_{\mathrm{eq}}}=\frac{1}{2}k\left[3\left(\frac{2L}{3}\right)^2-4L\left(\frac{2L}{3}\right)+2L^2\right]=\frac{1}{3}\,kL^2$

Y calculamos por fin la energía cinética máxima y la celeridad máxima:

$K_{\mathrm{max}}=E\,-\,U_{\mathrm{min}}=\frac{3}{8}\,kL^2-\frac{1}{3}\,kL^2=\frac{1}{24}\,kL^2\,\,\,\,\,\Longrightarrow\,\,\,\,\,\frac{1}{2}mv_{\mathrm{max}}^2=\frac{1}{24}\,kL^2\,\,\,\,\,\Longrightarrow\,\,\,\,\,v_{\mathrm{max}}^2=\frac{kL^2}{12\,m}\,\,\,\,\,\Longrightarrow\,\,\,\,\,v_{\mathrm{max}}=\sqrt{\frac{k}{3m}}\,\frac{L}{2}$

No Boletín - Partícula unida a dos muelles (Ex.Feb/14)

De Laplace

1 Enunciado

2 Posición de equilibrio

3 Celeridad máxima

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES