Entrar Página Discusión Historial Go to the site toolbox

No Boletín - Partícula que desliza apoyada sobre semiaro (Ex.Ene/16)

De Laplace

Contenido

1 Enunciado

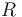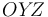Sea un semiaro fijo, de radio \,R\, y centro de curvatura \,O\,, contenido en el plano vertical \,OY\!Z\, (ver figura). La partícula 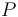\,P\, de masa 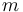\,m\,, inicialmente en reposo apoyada sobre el punto más alto del semiaro, sufre una leve perturbación y comienza a deslizar sobre él sin rozamiento y bajo la acción de su propio peso (aceleración gravitatoria: 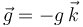\,\vec{g}=-g\,\vec{k}\,). El deslizamiento continúa hasta cierta posición en la que se observa que la partícula pierde el contacto con el semiaro. 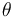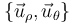Utilícese la coordenada acimutal \,\theta\, de la figura para describir la posición de la partícula sobre el semiaro, y la base polar \{\vec{u}_{\rho},\vec{u}_{\theta}\}\, para expresar las magnitudes vectoriales.

  1. Halle la celeridad de la partícula mientras desliza sobre el semiaro.
  2. Determine la fuerza de reacción vincular que el semiaro ejerce sobre la partícula durante su deslizamiento.
  3. ¿En qué posición pierde la partícula el contacto con el semiaro?

2 Celeridad durante el deslizamiento

Las fuerzas que actúan sobre la partícula 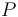\,P\, mientras desliza sobre el semiaro son dos: su propio peso 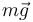\,m\vec{g}\, y la fuerza de reacción vincular 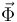\,\vec{\Phi}\, que le ejerce el semiaro. El peso 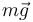\,m\vec{g}\, es una fuerza conservativa, y la fuerza vincular \vec{\Phi}\, no realiza trabajo sobre 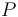\,P\, porque es siempre perpendicular a su desplazamiento (la fuerza vincular no trabaja en un vínculo liso y esclerónomo). En consecuencia, la energía mecánica 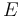\,E\, de la partícula (suma de su energía cinética 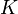K\, y su energía potencial 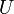U\,) se conservará constante en el tiempo (teorema de conservación de la energía mecánica):

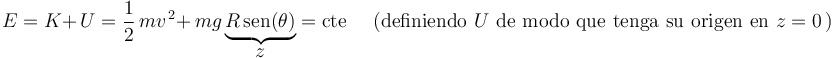
E=K+\,U=\frac{1}{2}\,mv^{\, 2}+\,mg\underbrace{R\,\mathrm{sen}(\theta)}_{\displaystyle z}=\mathrm{cte}\,\,\,\,\,\,\,\,\mathrm{(definiendo}\,\,U\,\,\mathrm{de}\,\,\mathrm{modo}\,\,\mathrm{que}\,\,\mathrm{tenga}\,\,\mathrm{su}\,\,\mathrm{origen}\,\,\mathrm{en}\,\,z=0\,\mathrm{)}

El valor constante de 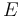\,E\, se determina evaluando su expresión para las condiciones iniciales dadas 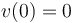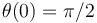\,v(0)=0\,, \,\,\theta(0)=\pi/2\, (la partícula en reposo sobre el punto más alto del semiaro):

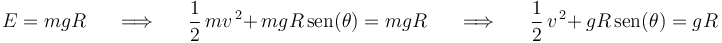
E=mgR \,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\,\frac{1}{2}\,mv^{\, 2}+\,mgR\,\mathrm{sen}(\theta)=mgR\,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\,\frac{1}{2}\,v^{\, 2}+\,gR\,\mathrm{sen}(\theta)=gR

de donde se deduce que la celeridad 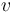\,v\, de la partícula durante el deslizamiento vale:

v=\sqrt{2\,gR\,[1-\mathrm{sen}(\theta)\,]}

3 Fuerza de reacción vincular durante el deslizamiento

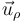Dado que el vínculo es liso (sin rozamiento), la fuerza vincular \vec{\Phi}\, es perpendicular al propio vínculo y, por tanto, tiene dirección radial \,\vec{u}_{\rho}\,. Expresadas en la base polar, las dos fuerzas actuantes sobre la partícula durante su deslizamiento sobre el semiaro son:

\left\{\begin{array}{l} m\vec{g}=-mg\,\vec{k}=-mg\,[\,\mathrm{sen}(\theta)\,\vec{u}_{\rho}+\mathrm{cos}(\theta)\,\vec{u}_{\theta}\,] \\ \\ \vec{\Phi}=\Phi\,\vec{u}_{\rho} \end{array}\right.

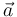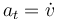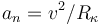La aceleración \,\vec{a}\, de la partícula durante su deslizamiento la expresamos primero en la base de Frenet (componentes intrínsecas de la aceleración: a_t=\dot{v}\, y \,a_n=v^2/R_{\kappa}\,), y después la pasamos a la base polar (teniendo presente que en este caso 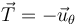\,\vec{T}=-\vec{u}_{\theta}\, y \,\vec{N}=-\vec{u}_{\rho}\,):

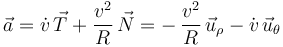
\,\vec{a}=\dot{v}\,\vec{T}+\frac{v^2}{R}\,\vec{N}=-\,\frac{v^2}{R}\,\vec{u}_{\rho}-\dot{v}\,\vec{u}_{\theta}

Proyectando la segunda ley de Newton 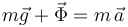    m\vec{g}+\vec{\Phi}=m\,\vec{a}     sobre la dirección radial 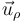\,\vec{u}_{\rho}\,, se obtiene la siguiente ecuación escalar:

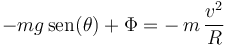
-mg\,\mathrm{sen}(\theta)+\Phi=-\,m\,\frac{v^2}{R}

La fuerza de reacción vincular 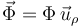\,\vec{\Phi}=\Phi\,\vec{u}_{\rho}\,, que ejerce el semiaro sobre la partícula durante su deslizamiento, queda determinada por el valor de 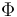\,\Phi\, que se obtiene despejando en la anterior ecuación:

\Phi=m\!\left[g\,\mbox{sen}(\theta)-\displaystyle\frac{v^2}{R}\right]

y sustituyendo la expresión de la celeridad     \,v=\sqrt{2\,gR\,[1-\mathrm{sen}(\theta)\,]}\,     del apartado anterior:

\Phi=mg \left[\,3\,\mathrm{sen}(\theta)-2\,\right]

4 Posición de pérdida del contacto partícula-semiaro

Mientras desliza, la partícula 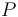\,P\, se halla en contacto con el semiaro, pero sólo está apoyada sobre él. El semiaro impedirá que la partícula lo atraviese de fuera a dentro, pero no podrá evitar que en cierto instante la partícula pierda el contacto con él y lo abandone (se trata de un vínculo unilateral). Esto se traduce matemáticamente en que la fuerza vincular 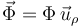\,\vec{\Phi}=\Phi\,\vec{u}_{\rho}\, sólo puede estar dirigida hacia fuera del semiaro, nunca hacia dentro. Dicho de otro modo, la componente radial \,\Phi\, de la citada fuerza debe ser siempre mayor o igual que cero, condición que restringe el intervalo de valores posibles de \,\theta:

\Phi=mg\left[\,3\,\mathrm{sen}(\theta)-2\,\right]\geq 0\,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\,\mathrm{sen}(\theta)\geq\frac{2}{3}\,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\,90^{\, o}\geq \theta\geq 41,8^{\, o}

Por tanto, cuando alcanza la posición 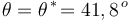\,\theta=\theta^{\, *}\!=41,8^{\, o}\, en la que 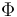\,\Phi\, se anula, la partícula pierde el contacto con el semiaro:

\mathrm{Cuando}\,\,\,\,\theta=\theta^{\, *}\!=41,8^{\, o}\,\,\,\,\,\longrightarrow\,\,\,\,\,\mathrm{sen}(\theta^{\, *})=\frac{2}{3}\,\,\,\,\,\,\,\,\,\longrightarrow\,\,\,\,\,\,\,\,\, \Phi=mg\left[\,3\,\mathrm{sen}(\theta^{\, *})-2\,\right]= 0 \,\,\,\,\,\longrightarrow\,\,\,\,\,P\,\,\mathrm{pierde}\,\,\mathrm{el}\,\,\mathrm{contacto}\,\,\mathrm{con}\,\,\mathrm{el}\,\,\mathrm{semiaro}
Obtenido de "http://tesla.us.es/wiki/index.php/No_Bolet%C3%ADn_-_Part%C3%ADcula_que_desliza_apoyada_sobre_semiaro_(Ex.Ene/16)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 13:59, 14 mar 2016. - Esta página ha sido visitada 3.793 veces. - Aviso legal - Acerca de Laplace