No Boletín - Partícula en varilla ranurada móvil (Ex.Ene/20)

De Laplace

1 Enunciado

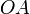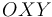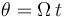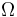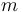La varilla $OA\,$ , ranurada longitudinalmente y contenida en el plano horizontal $OXY\,$ , rota alrededor del eje fijo $OZ\,$ de tal modo que el ángulo que forma la misma con el eje $OX\,$ viene dado en función del tiempo por la expresión $\,\theta=\Omega\, t\,$ (donde $\,\Omega\,$ es una constante conocida). Una partícula $P\,$ de masa $m\,$ se encuentra confinada en la ranura de la citada varilla, pudiendo deslizar sin rozamiento a lo largo de ella, y estando sometida a la acción de un resorte elástico (de constante 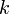$k\,$ y longitud natural nula) con anclaje en el punto fijo 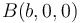$B(b,0,0)\,$ . 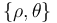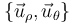En la figura se definen las coordenadas polares $\{\rho,\theta\}\,$ de la partícula $P\,$ , así como la base ortonormal $\{\vec{u}_{\rho},\vec{u}_{\theta}\}\,$ asociada a las mismas. 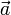En lo que sigue, denominaremos $\vec{v}\,$ y $\vec{a}\,$ , respectivamente, a la velocidad y a la aceleración de la partícula $P\,$ respecto al triedro fijo $OXYZ\,$ .

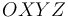Nota: Obsérvese que la varilla 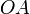$OA\,$ constituye un vínculo liso y reónomo sobre la partícula $P\,$ .

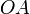¿Cuál de las siguientes condiciones ha de ser verificada en todo instante por la fuerza vincular $\vec{\Phi}\,$ que ejerce la varilla $OA\,$ sobre la partícula $P\,$ ? $\mathrm{(1)}\,\,\,\vec{\Phi}\cdot\vec{u}_{\theta}=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(2)}\,\,\,\vec{\Phi}\cdot\vec{v}=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(3)}\,\,\,\vec{\Phi}\cdot\vec{u}_{\rho}=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(4)}\,\,\,\vec{\Phi}\times\vec{a}=\vec{0}$
Proyectando la segunda ley de Newton sobre la dirección radial 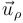$\vec{u}_{\rho}\,$ , deduzca la ecuación diferencial que debe satisfacer la función 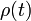$\rho(t)\,$ que da la coordenada radial de la partícula $P\,$ en cada instante.
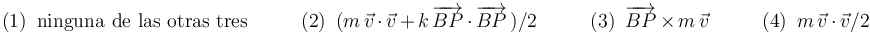
¿Cuál de las siguientes magnitudes físicas conserva su valor constante durante el movimiento de la partícula? $\mathrm{(1)}\,\,\,\mathrm{ninguna}\,\,\mathrm{de}\,\,\mathrm{las}\,\,\mathrm{otras}\,\,\mathrm{tres}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(2)}\,\,\,(m\,\vec{v}\,\cdot\,\vec{v}\,+\,k\,\overrightarrow{BP}\,\cdot\,\overrightarrow{BP}\,)/2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(3)}\,\,\,\overrightarrow{BP}\,\times\, m\,\vec{v}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(4)}\,\,\,m\,\vec{v}\,\cdot\,\vec{v}/2$

2 Segunda ley de Newton: ecuación de movimiento y fuerza vincular

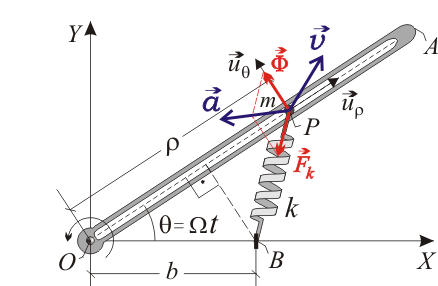
El movimiento tiene lugar en un plano horizontal y, en consecuencia, no hay que considerar efecto gravitatorio. Sobre la partícula 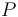$\,P\,$ actúan dos fuerzas: una de naturaleza activa (la fuerza elástica 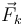$\,\vec{F}_k\,$ ejercida por el resorte) y otra de tipo vincular (la fuerza 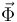$\,\vec{\Phi}\,$ ejercida por la varilla ranurada).

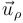Dado que el vínculo es liso (sin rozamiento), la ranura de la varilla no tiene la capacidad de ejercer fuerzas tangenciales a su propia dirección. Por tanto, la fuerza vincular $\vec{\Phi}\,$ es perpendicular a la dirección radial $\vec{u}_{\rho}\,$ de la ranura en la que se encuentra confinada la partícula, debiendo satisfacer en todo instante la condición:

$\mathrm{vinculo}\,\,\mathrm{liso}\,\,\,\,\,\,\,\,\,\,\longrightarrow\,\,\,\,\,\,\,\,\,\,\vec{\Phi}\perp\mathrm{vinculo}\,\,\,\,\,\,\,\,\,\,\longrightarrow\,\,\,\,\,\,\,\,\,\,\vec{\Phi}\perp\vec{u}_{\rho} \,\,\,\,\,\,\,\,\,\,\Longrightarrow\,\,\,\,\,\,\,\,\,\,\vec{\Phi}\,\cdot\,\vec{u}_{\rho}= 0$

Así que la opción (3) es la respuesta correcta a la primera pregunta del ejercicio.

Las expresiones analíticas de las dos fuerzas en la base polar son las siguientes:

$\left\{\begin{array}{l} \vec{F}_k=-\,k\,\overrightarrow{BP}=-\,k\,\{[\,\rho\,-\,b\,\mathrm{cos}(\Omega\, t)]\,\vec{u}_{\rho}\,+\,b\,\mathrm{sen}(\Omega\, t)\,\vec{u}_{\theta}\}= \\ \\ \vec{\Phi}=\Phi\,\vec{u}_{\theta} \end{array}\right.$

La velocidad y la aceleración de la partícula expresadas en la base polar vienen dadas en general por:

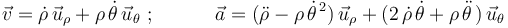
$\vec{v}=\dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}=(\ddot{\rho}-\rho\,\dot{\theta}^{\, 2})\,\vec{u}_{\rho}+(2\,\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta}\,)\,\vec{u}_{\theta}$

pero al particularizar, teniendo en cuenta la ecuación del vínculo: 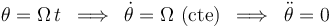$\,\,\theta=\Omega\, t\,\,\,\Longrightarrow\,\,\,\dot{\theta}=\Omega\,\,\mathrm{(cte)}\,\,\,\Longrightarrow\,\,\,\ddot{\theta}=0\,$ , queda:

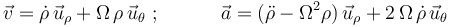
$\vec{v}=\dot{\rho}\,\vec{u}_{\rho}+\Omega\,\rho\,\vec{u}_{\theta} \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}=(\ddot{\rho}-\Omega^2\rho)\,\vec{u}_{\rho}+2\,\Omega\,\dot{\rho}\,\vec{u}_{\theta}$

Planteamos la segunda ley de Newton: 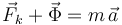$\vec{F}_k+\vec{\Phi}=m\,\vec{a}$ y la proyectamos sobre las direcciones radial y acimutal, obteniendo dos ecuaciones escalares:

$\left\{\begin{array}{l} -\,k\,[\,\rho\,-\,b\,\mathrm{cos}(\Omega\, t)\,]=m(\,\ddot{\rho}-\Omega^2\rho\,)\,\,\,\,\,\,\,\,\,\, (1) \\ \\ -\,k\,b\,\mathrm{sen}(\Omega\, t)+\Phi=2\,m\,\Omega\,\dot{\rho}\,\,\,\,\,\,\,\,\,\, (2) \end{array}\right.$

La ecuación (1) nos proporciona la ecuación diferencial de segundo orden que debe satisfacer la función 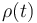$\,\rho(t)$ :

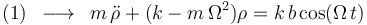
$\mathrm{(1)}\,\,\,\longrightarrow\,\,\,m\,\ddot{\rho}+(k-m\,\Omega^2)\rho=k\,b\,\mathrm{cos}(\Omega\, t)$

que constituye la respuesta a la segunda pregunta del ejercicio.

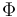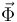La fuerza vincular que ejerce la varilla ranurada sobre la partícula se obtiene despejando $\,\Phi\,\,$ en la ecuación (2) y sustituyendo en la expresión vectorial de $\,\vec{\Phi}\,$ :

$\mathrm{(2)}\,\,\,\longrightarrow\,\,\,\Phi=2\,m\,\Omega\,\dot{\rho}+k\,b\,\mathrm{sen}(\Omega\, t) \,\,\,\Longrightarrow\,\,\,\vec{\Phi}=\left[\,2\,m\,\Omega\,\dot{\rho}+k\,b\,\mathrm{sen}(\Omega\, t)\,\right] \,\vec{u}_{\theta}$

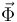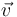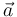Volviendo a la primera pregunta del ejercicio, cabe señalar que, una vez determinadas las expresiones de $\,\vec{\Phi}\,$ , $\,\vec{v}\,$ y $\,\vec{a}\,$ en la base polar, resulta trivial comprobar analíticamente que las respuestas (1), (2) y (4) son falsas:

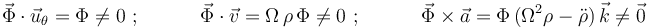
$\vec{\Phi}\cdot\vec{u}_{\theta}=\Phi\neq 0 \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{\Phi}\cdot\vec{v}=\Omega\,\rho\,\Phi \neq 0 \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{\Phi}\times\vec{a}=\Phi\, (\Omega^2\rho-\ddot{\rho})\,\vec{k}\neq\vec{0}$

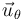Además, dado que las igualdades expresadas en las respuestas (1), (2) y (4) corresponden geométricamente a ciertas condiciones de ortogonalidad o paralelismo entre vectores, también es posible su descarte inspeccionando la figura que acompaña a la presente solución. En efecto, en dicha figura se observa que la fuerza vincular $\vec{\Phi}\,$ no es perpendicular a la dirección acimutal $\vec{u}_{\theta}\,$ , ni perpendicular a la velocidad $\vec{v}\,$ , ni paralela a la aceleración $\vec{a}\,$ . 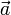Nótese que, en coherencia con la segunda ley de Newton, la aceleración se ha representado en la citada figura con la misma dirección y sentido que la resultante de las fuerzas actuantes sobre la partícula.

3 ¿Conserva su valor constante alguna de las magnitudes propuestas en la tercera pregunta?

Para responder la última pregunta del ejercicio, lo primero que hacemos es identificar las magnitudes físicas propuestas. Se trata de la energía cinética 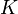$K\,$ en la opción (4), la energía mecánica 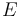$E\,$ en la opción (2), y el momento cinético 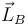$\vec{L}_B\,$ en la opción (3):

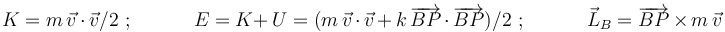
$K=m\,\vec{v}\,\cdot\,\vec{v}/2 \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, E=K+\, U=(m\,\vec{v}\,\cdot\,\vec{v}\,+\,k\,\overrightarrow{BP}\,\cdot\,\overrightarrow{BP})/2 \,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \vec{L}_B=\overrightarrow{BP}\,\times\, m\,\vec{v}$

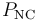Los teoremas de la energía cinética (T.E.C.), de la energía mecánica (T.E.M.) y del momento cinético (T.M.C.) establecen que las derivadas temporales de estas magnitudes son iguales, respectivamente, a la potencia instantánea $P\,$ desarrollada sobre la partícula, a la potencia instantánea no conservativa $P_{\mathrm{NC}}\,$ desarrollada sobre la misma, y al momento resultante 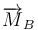$\overrightarrow{M}_B\,$ de las fuerzas actuantes:

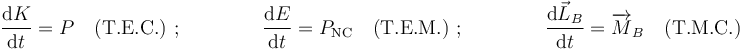
$\frac{\mathrm{d}K}{\mathrm{d}t}=P\,\,\,\,\,\,\mathrm{(T.E.C.)}\,\,; \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{\mathrm{d}E}{\mathrm{d}t}=P_{\mathrm{NC}}\,\,\,\,\,\,\mathrm{(T.E.M.)}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \frac{\mathrm{d}\vec{L}_B}{\mathrm{d}t}=\overrightarrow{M}_B\,\,\,\,\,\,\mathrm{(T.M.C.)}$

A partir de estos tres teoremas, se deducen los correspondientes teoremas de conservación:

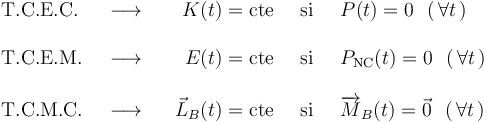
$\begin{array}{llrll} \mathrm{T.C.E.C.} & \,\,\,\longrightarrow\,\,\,\,\, & K(t)=\mathrm{cte} & \,\,\,\mathrm{si}\,\,\, & P(t)=0\,\,\,\,(\,\forall t\,) \\ \\ \mathrm{T.C.E.M.} & \,\,\,\longrightarrow\,\,\,\,\, & E(t)=\mathrm{cte} & \,\,\,\mathrm{si}\,\,\, & P_{\mathrm{NC}}(t)=0\,\,\,\,(\,\forall t\,) \\ \\ \mathrm{T.C.M.C.} & \,\,\,\longrightarrow\,\,\,\,\, & \vec{L}_B(t)=\mathrm{cte} & \,\,\,\mathrm{si}\,\,\, & \overrightarrow{M}_B(t)=\vec{0}\,\,\,\,(\,\forall t\,) \end{array}$

Sin embargo, vamos a comprobar que ninguna de las tres magnitudes propuestas se conserva constante en el presente ejercicio.

En primer lugar, la energía cinética de la partícula no es constante en el tiempo porque tanto la fuerza elástica (conservativa) como la fuerza vincular (no conservativa) desarrollan potencia sobre la partícula:

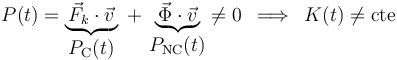
$P(t)=\underbrace{\,\vec{F}_k\cdot\vec{v}\,}_{\displaystyle P_{\mathrm{C}}(t)}\,\,+\,\underbrace{\,\vec{\Phi}\cdot\vec{v}\,}_{\displaystyle P_{\mathrm{NC}}(t)}\neq 0\,\,\,\Longrightarrow\,\,\,K(t)\neq\mathrm{cte}$

Que la fuerza elástica trabaja (desarrolla potencia) es evidente porque la elongación del resorte va variando a lo largo del movimiento de la partícula. El hecho de que la fuerza vincular también trabaje se debe al carácter móvil (reónomo) del vínculo, que es la causa de que la velocidad de la partícula tenga una componente de arrastre en la dirección de la propia fuerza vincular (cosa que no ocurre en los vínculos fijos o esclerónomos). Es frecuente el error de creer que todos los vínculos lisos no trabajan. La realidad es que los lisos esclerónomos no trabajan, pero los lisos reónomos sí trabajan.

En segundo lugar, la energía mecánica de la partícula tampoco se conserva constante, ya que, tal como hemos comentado, la fuerza vincular desarrolla potencia no conservativa sobre la partícula:

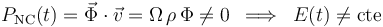
$P_{\mathrm{NC}}(t)=\vec{\Phi}\cdot\vec{v}=\Omega\,\rho\,\Phi\neq 0\,\,\,\Longrightarrow\,\,\,E(t)\neq\mathrm{cte}$

Por último, el momento cinético de la partícula respecto al punto B tampoco se conserva constante en el tiempo. Aunque la fuerza elástica es central con centro en B, la fuerza vincular no lo es, y esto provoca que el momento resultante de fuerzas respecto al punto B sea distinto de cero:

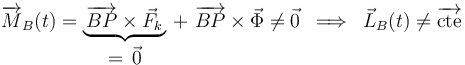
$\overrightarrow{M}_B(t)=\underbrace{\,\overrightarrow{BP}\times\vec{F}_k\,}_{\displaystyle =\,\vec{0}}\,+\,\,\overrightarrow{BP}\times\vec{\Phi}\neq \vec{0}\,\,\,\Longrightarrow\,\,\,\vec{L}_B(t)\neq\overrightarrow{\mathrm{cte}}$

Así, pues, llegamos a la conclusión anunciada de que ninguna de las tres magnitudes propuestas en la tercera pregunta del ejercicio se conserva constante durante el movimiento de la partícula, y en consecuencia la respuesta correcta a dicha pregunta es la opción (1): "ninguna de las otras tres".

No Boletín - Partícula en varilla ranurada móvil (Ex.Ene/20)

De Laplace

1 Enunciado

2 Segunda ley de Newton: ecuación de movimiento y fuerza vincular

3 ¿Conserva su valor constante alguna de las magnitudes propuestas en la tercera pregunta?

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES