No Boletín - Partícula cae por rampa e impacta en muelle (Ex.Sep/12)
De Laplace
1 Enunciado
Una partícula de masa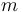 
desliza sin rozamiento a lo largo de una rampa bajo el efecto de su propio peso. En el instante inicial, la partícula se halla en reposo en el punto más alto de la rampa, a una altura 
. Al final de la rampa y apoyado sobre ella, hay un resorte elástico OA de constante recuperadora 
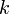y longitud natural 
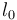. Su extremo O está fijo (punto de anclaje), y
su extremo libre A descansa sobre la rampa, a una altura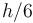 
cuando el resorte está relajado.
- ¿Con qué celeridad
entrará en contacto la partícula con el extremo A del resorte?
- ¿Cuánto vale la constante 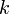del resorte si la partícula llega hasta el final de la rampa (punto O) con celeridad nula?
2 Celeridad al entrar en contacto con el resorte
Distinguiremos dos etapas en el movimiento de la partícula: antes de entrar en contacto con el muelle, y después de entrar en contacto con el muelle. Al no haber rozamiento, sabemos que en la primera etapa sólo actúan dos fuerzas sobre la partícula: su peso (fuerza conservativa) y la reacción normal de la rampa. La reacción normal no realiza trabajo sobre la partícula porque es perpendicular a su trayectoria. Por tanto, conforme al teorema de conservación de la energía mecánica (la única fuerza que trabaja es conservativa), la energía mecánica (= energía cinética + energía potencial gravitatoria) ha de conservarse constante en el tiempo:
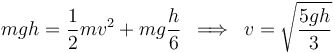
donde hemos llamado a la celeridad de la partícula en el instante en que entra en contacto con el muelle, y hemos exigido la igualdad de energías mecánicas entre el instante inicial y el instante de entrada en contacto partícula-muelle.
3 Valor de la constante elástica del resorte
En la segunda etapa del movimiento de la partícula, aparece una nueva fuerza que trabaja pero también es conservativa: la fuerza elástica ejercida por el muelle. Por tanto, la energía mecánica (= energía cinética + energía potencial gravitatoria + energía potencial elástica) seguirá conservándose constante en el tiempo:
donde hemos exigido la igualdad de energías mecánicas entre el instante inicial y el instante de llegada de la partícula al final de la rampa (sin energía cinética, sin energía potencial gravitatoria, y sólo con la energía potencial elástica debida a la contracción del muelle).
