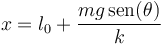No Boletín - Muelle en plano inclinado II (Ex.Ene/19)
De Laplace
Contenido |
1 Enunciado
Una partícula  , de masa
, de masa 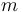 , desliza sin rozamiento a lo largo de una rampa de inclinación
, desliza sin rozamiento a lo largo de una rampa de inclinación  respecto a la horizontal. Durante su movimiento, la partícula
respecto a la horizontal. Durante su movimiento, la partícula  está sometida a la acción de su propio peso y es solicitada desde un punto fijo
está sometida a la acción de su propio peso y es solicitada desde un punto fijo  (ver figura) mediante un resorte elástico
(ver figura) mediante un resorte elástico  de constante recuperadora
de constante recuperadora 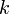 y longitud natural
y longitud natural 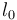 . Se describe la posición de la partícula
. Se describe la posición de la partícula  mediante su coordenada
mediante su coordenada  en la escuadra
en la escuadra  de la figura.
de la figura.
- ¿Cuánto vale la fuerza vincular
 que la rampa ejerce sobre la partícula
que la rampa ejerce sobre la partícula  ?
?
- ¿Qué ecuación diferencial satisface la función
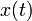 que describe la posición de la partícula
que describe la posición de la partícula  en cada instante?
en cada instante?
- ¿Cuál es la posición de equilibrio de la partícula
 ?
?
2 Segunda ley de Newton (fuerza vincular y ecuación diferencial de segundo orden)
Sobre la partícula  actúan dos fuerzas de naturaleza activa (su peso
actúan dos fuerzas de naturaleza activa (su peso 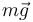 y la fuerza elástica
y la fuerza elástica 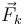 que le ejerce el resorte) y una fuerza de reacción vincular (la fuerza
que le ejerce el resorte) y una fuerza de reacción vincular (la fuerza 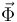 que le ejerce la rampa). La fuerza
que le ejerce la rampa). La fuerza 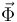 tiene la dirección perpendicular a la superficie de la rampa (no hay rozamiento) y su sentido es hacia el exterior de la rampa (vínculo unilateral). Las expresiones analíticas de las tres fuerzas en la base cartesiana propuesta son las siguientes:
tiene la dirección perpendicular a la superficie de la rampa (no hay rozamiento) y su sentido es hacia el exterior de la rampa (vínculo unilateral). Las expresiones analíticas de las tres fuerzas en la base cartesiana propuesta son las siguientes:
![\left\{\begin{array}{l} m\vec{g}=mg\,[\,\mathrm{sen}(\theta)\,\vec{\imath}-\mathrm{cos}(\theta)\,\vec{\jmath}\,\,] \\ \\ \vec{F}_k=-k(x-l_0)\,\vec{\imath} \\ \\ \vec{\Phi}=\Phi\,\vec{\jmath} \end{array}\right.](/wiki/images/math/6/2/9/62955647881a1ef0343d000a213d8ab6.png)
La aceleración de la partícula expresada en la base cartesiana propuesta viene dada por:

Planteamos la segunda ley de Newton: 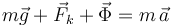 y la proyectamos sobre la base cartesiana propuesta, obteniendo dos ecuaciones escalares:
y la proyectamos sobre la base cartesiana propuesta, obteniendo dos ecuaciones escalares:
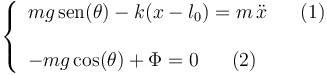
El módulo 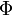 de la fuerza vincular se obtiene despejando en la ecuación (2):
de la fuerza vincular se obtiene despejando en la ecuación (2):

Por tanto, la fuerza vincular que la rampa ejerce sobre la partícula viene dada por la expresión:
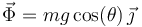
La ecuación (1) nos proporciona la ecuación diferencial de segundo orden que debe satisfacer la función 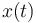 :
:
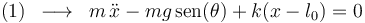
3 Integral primera del movimiento (ecuación diferencial de primer orden)
La fuerza vincular  no trabaja sobre la partícula por ser siempre perpendicular a su desplazamiento (vínculo liso y esclerónomo). Así que las dos fuerzas que trabajan sobre la partícula (su peso y la fuerza elástica) son conservativas, y por tanto se conserva constante en el tiempo su energía mecánica
no trabaja sobre la partícula por ser siempre perpendicular a su desplazamiento (vínculo liso y esclerónomo). Así que las dos fuerzas que trabajan sobre la partícula (su peso y la fuerza elástica) son conservativas, y por tanto se conserva constante en el tiempo su energía mecánica  (suma de su energía cinética
(suma de su energía cinética  y sus energías potenciales gravitatoria
y sus energías potenciales gravitatoria 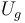 y elástica
y elástica 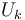 ). Dicho de otro modo, el teorema de conservación de la energía mecánica nos permite deducir que
). Dicho de otro modo, el teorema de conservación de la energía mecánica nos permite deducir que 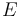 es una integral primera del movimiento de la partícula:
es una integral primera del movimiento de la partícula:

Abordemos ahora la tarea de expresar la energía mecánica como una función de 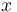 y
y 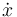 .
.
La velocidad de la partícula expresada en la base cartesiana propuesta viene dada por:
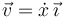
Así que la energía cinética de la partícula vale:
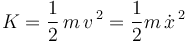
Por otra parte, la energía potencial gravitatoria de la partícula es:
![U_g=mg[-x\,\mathrm{sen}(\theta)]\,=-mg\,\mathrm{sen}(\theta)\, x](/wiki/images/math/d/a/9/da9808a7a9bacc2726f2977e3f0c3115.png)
Obsérvese que la expresión propuesta para 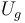 corresponde a tomar el origen de energía potencial gravitatoria en
corresponde a tomar el origen de energía potencial gravitatoria en 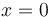 , siendo
, siendo ![[-x\,\mathrm{sen}(\theta)]\,](/wiki/images/math/1/0/f/10f5b8ee38967d31dfd45a6b7cd58e24.png) la altura de la partícula respecto a dicho origen (nótese que el eje
la altura de la partícula respecto a dicho origen (nótese que el eje  apunta hacia abajo).
apunta hacia abajo).
Por último, la energía potencial elástica de la partícula es:
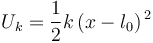
La suma de energía cinética y energía potencial total nos da como resultado la energía mecánica de la partícula:

Desde un punto de vista matemático, la integral primera que acabamos de obtener nos proporciona una ecuación diferencial de primer orden que debe ser satisfecha por la función 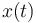 :
:
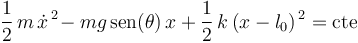
Puede comprobarse que, derivando respecto al tiempo esta ecuación diferencial de primer orden (y simplificando), se llega a la ecuación diferencial de segundo orden que se obtuvo a partir de la segunda ley de Newton en el apartado anterior.
Por tanto, ante la pregunta de cuál es la ecuación diferencial que debe satisfacer la función 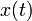 , es igualmente correcto responder con la ecuación diferencial de segundo orden obtenida en el apartado anterior o con la ecuación diferencial de primer orden obtenida en el presente apartado.
, es igualmente correcto responder con la ecuación diferencial de segundo orden obtenida en el apartado anterior o con la ecuación diferencial de primer orden obtenida en el presente apartado.
4 Posición de equilibrio
La condición de equilibrio mecánico para una partícula consiste en la nulidad de la fuerza neta que actúa sobre ella:  . Y proyectando esta ecuación vectorial sobre la dirección del eje
. Y proyectando esta ecuación vectorial sobre la dirección del eje  , se obtiene la siguiente ecuación escalar:
, se obtiene la siguiente ecuación escalar:
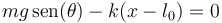
Y despejando en dicha ecuación, se obtiene la posición de equilibrio de la partícula: