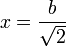No Boletín - Movimiento rectilíneo por tramos

De Laplace

Contenido

1 Enunciado
2 Energía potencial
- 2.1 Región x>b
- 2.2 Región x<b
3 Energía mecánica
4 Punto de retorno

1 Enunciado

Una partícula de masa $m$ , realiza un movimiento rectilíneo sobre la parte positiva de un eje cartesiano OX. Cuando la distancia entre la partícula y el origen $O$ supera una cierta longitud $b$ conocida, la partícula es atraída hacia $O$ por una fuerza de módulo $m k / x 2$ (siendo $k$ una constante); pero, sin embargo, cuando $x < b$ , la partícula es repelida desde $O$ por una fuerza de módulo $m b k / x 3$ .

Determine y represente gráficamente la energía potencial de la partícula en función de su coordenada $x$ (considerando que dicha función es nula en el infinito y exigiendo su continuidad en $x = b$ ).
Sabiendo que la partícula inicia su movimiento desde el reposo instantáneo en el punto $P 0$ de coordenada $x = 2 b$ , determine su energía mecánica.
¿En qué otro punto alcanzará la partícula el reposo instantáneo (punto de retorno)?

2 Energía potencial

Obtenemos la energía potencial integrando la fuerza desde el infinito hasta una cierta posición. Dado que la fuerza está definida por tramos, debemos distinguir dos casos.

2.1 Región x>b

La fuerza en esta región es atractiva, por lo que su sentido es hacia el origen y

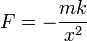
$F = -\frac{mk}{x^2}$

Integrando esta cantidad desde el infinito hasta un cierto valor de x

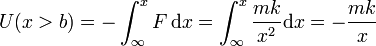
$U(x>b) = -\int_{\infty}^x F\,\mathrm{d}x=\int_{\infty}^x \frac{mk}{x^2}\mathrm{d}x = -\frac{mk}{x}$

2.2 Región x<b

En la región cercana al origen, la fuerza es repulsiva

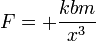
$F = +\frac{kbm}{x^3}$

Para hallar la energía potencial en esta región debemos integrar de nuevo desde el infinito hasta un cierto valor de x, pero al hacerlo debemos tener en cuenta que para recorrer este camino debemos pasar por toda la región $x > b$ . Por ello, debemos descomponer la integral en dos tramos

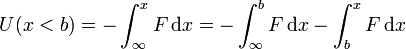
$U(x<b) = -\int_{\infty}^x F\,\mathrm{d}x = -\int_{\infty}^b F\,\mathrm{d}x- \int_{b}^xF\,\mathrm{d}x$

Para la primera integral debemos emplear la fuerza exterior

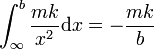
$\int_{\infty}^b \frac{mk}{x^2}\mathrm{d}x = -\frac{mk}{b}$

y para la segunda la interior

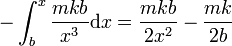
$-\int_{b}^x \frac{mkb}{x^3}\mathrm{d}x = \frac{mkb}{2x^2}-\frac{mk}{2b}$

Sumando las dos contribuciones

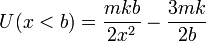
$U(x<b) = \frac{mkb}{2x^2}-\frac{3mk}{2b}$

Reuniendo este resultado con el de la sección anterior

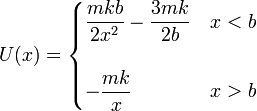
$U(x) = \begin{cases}\displaystyle \frac{mkb}{2x^2}-\frac{3mk}{2b} & x< b \\ & \\ \displaystyle -\frac{mk}{x} & x> b \end{cases}$

3 Energía mecánica

En un punto de reposo instantáneo, la energía cinética es nula

$K=0\,$

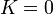
y la potencial la obtenemos sustituyendo el valor de la posición. Puesto que $2 b > b$

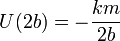
$U(2b) = -\frac{km}{2b}$

la energía mecánica es la suma de estas dos

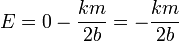
$E = 0 -\frac{km}{2b}=-\frac{km}{2b}$

4 Punto de retorno

El segundo punto de retorno es aquél para el cual la energía cinética vuelve a anularse y la energía mecánica coincide con la potencial. Este punto estará en la región $x < b$ . Igualando