No Boletín - Movimiento en espiral descrito en polares III (Ex.Nov/16)

De Laplace

1 Enunciado

El movimiento de cierta partícula en el plano 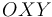$OXY\,$ viene dado en coordenadas polares mediante las ecuaciones horarias:

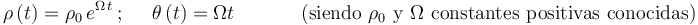
$\rho\,(t)=\rho_{0}\,e^{\Omega\, t}\,;\,\,\,\,\,\,\,\,\theta\,(t)=\Omega t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathrm{(siendo}\,\,\rho_{0}\,\,\mathrm{y}\,\,\Omega\,\,\mathrm{constantes}\,\,\mathrm{positivas}\,\,\mathrm{conocidas)}$

Al expresar en la base polar la velocidad ( 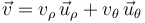$\vec{v}=v_{\rho}\,\vec{u}_{\rho}+v_{\theta}\,\vec{u}_{\theta}\,$ ) y la aceleración ( 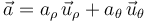$\vec{a}=a_{\rho}\,\vec{u}_{\rho}+a_{\theta}\,\vec{u}_{\theta}\,$ ) de la citada partícula, una de las cuatro componentes resulta ser nula en todo instante de tiempo. ¿Cuál de ellas?
Determine el vector normal $\vec{N}\,$ del triedro intrínseco de la trayectoria de la partícula.

2 Velocidad y aceleración en la base polar

La velocidad y la aceleración de la partícula en la base polar vienen dadas por la expresiones:

$\begin{array}{l} \vec{v}=\dot{\rho}\,\vec{u}_{\rho}+\rho\,\dot{\theta}\,\vec{u}_{\theta} \\ \\ \vec{a}=\left(\ddot{\rho}-\rho\,{\dot{\theta}}^{\, 2}\right)\vec{u}_{\rho}+\left(2\dot{\rho}\,\dot{\theta}+\rho\,\ddot{\theta}\,\right)\vec{u}_{\theta} \end{array}$

Por tanto, calculamos las derivadas primera y segunda respecto al tiempo de las ecuaciones horarias:

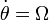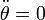
$\dot{\rho}=\Omega\rho$ ; $\ddot{\rho}=\Omega^{\, 2}\!\rho$ ; $\dot{\theta}=\Omega$ ; $\ddot{\theta}=0$

y, sustituyendo en las expresiones de arriba, obtenemos la velocidad de la partícula, su celeridad (módulo de la velocidad) y su aceleración:

$\begin{array}{l} \vec{v} = \Omega\rho\,\vec{u}_{\rho}+\Omega\rho\,\vec{u}_{\theta} \,\,\longrightarrow\,\, v=|\vec{v}\,|=\sqrt{2}\,\Omega\rho \\ \\ \vec{a}=2\,\Omega^2\rho\,\vec{u}_{\theta} \end{array}$

Observamos, pues, que la componente nula en todo instante de tiempo es la aceleración radial $a_{\rho}\,$ .

3 Vector normal del triedro intrínseco

El vector tangente se obtiene por normalización del vector velocidad:

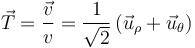
$\vec{T}=\frac{\vec{v}}{v}=\frac{1}{\sqrt{2}}\,(\vec{u}_{\rho}+\vec{u}_{\theta})$

La componente tangencial de la aceleración podemos obtenerla derivando la celeridad respecto al tiempo:

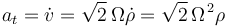
$a_t=\dot{v}=\sqrt{2}\,\Omega\dot{\rho}=\sqrt{2}\,\Omega^{\, 2}\rho$

Ahora determinamos el vector aceleración normal (restándole el vector aceleración tangencial al vector aceleración):

$\vec{a}_n=\vec{a}-\vec{a}_t=\vec{a}-a_t\,\vec{T}=2\,\Omega^{\, 2}\rho\,\vec{u}_{\theta}-\sqrt{2}\,\Omega^{\, 2}\rho\,\frac{1}{\sqrt{2}}\,(\vec{u}_{\rho}+\vec{u}_{\theta})=\Omega^{\, 2}\!\rho\,(-\,\vec{u}_{\rho}+\vec{u}_{\theta})$

Finalmente, el vector normal se puede obtener por normalización del vector aceleración normal:

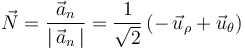
$\vec{N}=\frac{\vec{a}_n}{|\,\vec{a}_n\,|}=\frac{1}{\sqrt{2}}\,(-\,\vec{u}_{\rho}+\vec{u}_{\theta})$

Pero éste no es el único procedimiento posible para determinar el vector normal. Otra opción más directa consiste en obtenerlo por normalización de la derivada del vector tangente respecto a cualquier parámetro (por ejemplo, respecto a $\theta\,$ ):

$\frac{\mathrm{d}\vec{T}}{\mathrm{d}\theta}=\frac{1}{\sqrt{2}}\,(-\,\vec{u}_{\rho}+\vec{u}_{\theta})\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vec{N}=\frac{\mathrm{d}\vec{T}/\mathrm{d}\theta}{|\,\mathrm{d}\vec{T}/\mathrm{d}\theta\,|}=\frac{1}{\sqrt{2}}\,(-\,\vec{u}_{\rho}+\vec{u}_{\theta})$

donde se ha utilizado que, según se vio en la teoría, las derivadas respecto a $\theta\,$ de los vectores de la base polar valen:

$\frac{\mathrm{d}\vec{u}_{\rho}}{\mathrm{d}\theta}=\vec{u}_{\theta}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \frac{\mathrm{d}\vec{u}_{\theta}}{\mathrm{d}\theta}=-\,\vec{u}_{\rho}$

Un tercer procedimiento para calcular el vector normal es obtenerlo como producto vectorial del vector binormal y el vector tangente. Para lo cual, necesitamos determinar previamente el vector binormal (normalizando el producto vectorial de la velocidad y la aceleración de la partícula):

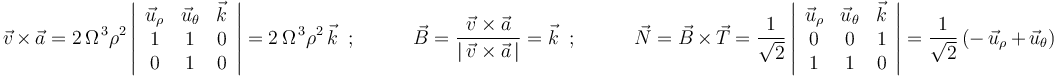
$\vec{v}\,\times\,\vec{a}=2\,\Omega^{\, 3}\rho^2\left|\begin{array}{ccc}\vec{u}_{\rho} & \vec{u}_{\theta} & \vec{k} \\ 1 & 1 & 0 \\ 0 & 1 & 0 \end{array}\right|=2\,\Omega^{\, 3}\rho^2\,\vec{k}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vec{B}=\frac{\vec{v}\times\vec{a}}{|\,\vec{v}\times\vec{a}\,|}=\vec{k}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\vec{N}=\vec{B}\,\times\,\vec{T}=\frac{1}{\sqrt{2}}\left|\begin{array}{ccc}\vec{u}_{\rho} & \vec{u}_{\theta} & \vec{k} \\ 0 & 0 & 1 \\ 1 & 1 & 0 \end{array}\right|=\frac{1}{\sqrt{2}}\,(-\,\vec{u}_{\rho}\,+\,\vec{u}_{\theta})$

Nota: Obsérvese que la base 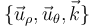$\{\vec{u}_{\rho}, \vec{u}_{\theta}, \vec{k}\}\,$ (denominada base cilíndrica) es ortonormal dextrógira, y por ese motivo los productos vectoriales de vectores expresados en la misma se realizan de forma análoga a como se realizan los productos vectoriales de vectores expresados en base cartesiana.

No Boletín - Movimiento en espiral descrito en polares III (Ex.Nov/16)

De Laplace

1 Enunciado

2 Velocidad y aceleración en la base polar

3 Vector normal del triedro intrínseco

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES