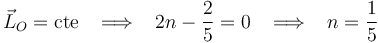No Boletín - Movimiento central en coordenadas polares (Ex.Dic/12)
De Laplace
1 Enunciado
El movimiento de una partícula en un plano 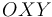 (para
(para 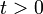 ) viene dado en coordenadas polares mediante las ecuaciones horarias:
) viene dado en coordenadas polares mediante las ecuaciones horarias:

donde 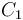 y
y 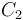 son constantes conocidas. Sabiendo que la fuerza que actúa sobre la partícula es central con centro en el origen de coordenadas, ¿cuál es necesariamente el valor del exponente
son constantes conocidas. Sabiendo que la fuerza que actúa sobre la partícula es central con centro en el origen de coordenadas, ¿cuál es necesariamente el valor del exponente 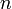 ?
?
2 Solución
Por ser la fuerza que actúa sobre la partícula una fuerza central con centro en el origen de coordenadas  , el momento de dicha fuerza respecto al punto
, el momento de dicha fuerza respecto al punto  es nulo. Y entonces sabemos que se conservará constante a lo largo del tiempo el momento cinético de la partícula respecto al punto
es nulo. Y entonces sabemos que se conservará constante a lo largo del tiempo el momento cinético de la partícula respecto al punto  (teorema de conservación del momento cinético de una partícula).
(teorema de conservación del momento cinético de una partícula).
Vamos, pues, a determinar primero dicho momento cinético 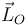 en función de los datos del ejercicio (entre ellos, el exponente
en función de los datos del ejercicio (entre ellos, el exponente 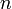 ), y después deduciremos el valor del exponente
), y después deduciremos el valor del exponente 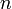 exigiendo que
exigiendo que 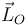 sea independiente del tiempo.
sea independiente del tiempo.
Sustituyendo las expresiones generales (en coordenadas polares) de los vectores de posición y velocidad de una partícula
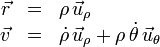
en la definición del momento cinético de la partícula respecto al origen de coordenadas  , se obtiene:
, se obtiene:
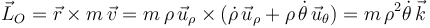
Y sustituyendo en esta expresión general las funciones concretas 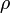 y
y 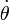 que se deducen de las ecuaciones horarias dadas en el enunciado, se llega a:
que se deducen de las ecuaciones horarias dadas en el enunciado, se llega a:
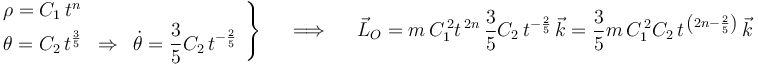
Finalmente, la exigencia de que 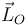 sea independiente del tiempo nos lleva a forzar la nulidad del exponente con que aparece el tiempo en la expresión obtenida, y de ahí obtenemos el valor de
sea independiente del tiempo nos lleva a forzar la nulidad del exponente con que aparece el tiempo en la expresión obtenida, y de ahí obtenemos el valor de 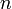 :
: