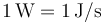No Boletín - Intensidad de una onda sonora (Ex.Nov/12)
De Laplace
1 Enunciado
La intensidad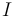 
de una onda sonora armónica propagándose en el seno de un gas puede calcularse mediante la fórmula:
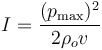
donde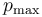 
es la amplitud de presión (dimensiones de presión), 
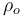es la densidad del gas en el equilibrio (se mide en kg/m3 en el SI), y 
es la velocidad de propagación de la onda.
- ¿Cuál es la ecuación dimensional de ?
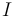- ¿En qué unidad se mide 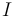en el SI?
2 Ecuación dimensional de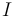
Tomando dimensiones en la fórmula facilitada, desaparece del denominador el factor numérico "2" por ser adimensional, y se obtiene:
![[I\,]=\frac{[p_{\mathrm{max}}]^2}{[\rho_o][v]}](/wiki/images/math/6/8/6/68644225550ed06d1264c071e4d0dc25.png)
El enunciado del ejercicio no nos informa de cuáles son las dimensiones de una presión (fuerza partido por superficie) y de una velocidad porque se considera que debemos conocerlas (aparecen en problemas de boletín hechos en clase):
![[p_{\mathrm{max}}]=\frac{[F\,]}{[S\,]}=\frac{MLT^{-2}}{L^2}=ML^{-1}T^{-2}\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
[v]=LT^{-1}](/wiki/images/math/1/b/8/1b820e9ed58683105281d0ed660c0742.png)
Sin embargo, sí se nos dice que la unidad SI de densidad es el kg/m3, lo cual nos permite deducir cuáles son las dimensiones de una densidad:
![\mathrm{unidad}\,\,\mathrm{SI}\,\,\mathrm{de}\,\, \rho_o = 1\,\mathrm{kg/m}^3\,\,\,\,\,\, \Longrightarrow \,\,\,\,\,\,[\rho_o]=ML^{-3}](/wiki/images/math/a/9/b/a9b91b048741efad8e89942365429238.png)
Sustituyendo las dimensiones de presión, velocidad y densidad, obtenemos al fin la ecuación dimensional de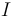 
:
![[I\,]=\frac{[p_{\mathrm{max}}]^2}{[\rho_o][v]}=\frac{(ML^{-1}T^{-2})^2}{ML^{-3}LT^{-1}}=MT^{-3}](/wiki/images/math/4/8/0/48047484e711d4e320d75f4f62bbf196.png)
3 Unidad de 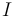en el SI
Una vez hallada la ecuación dimensional de 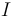, su unidad en el SI se deduce fácilmente a partir del correspondiente producto de potencias de las unidades de las magnitudes básicas en el SI:
![[I\,]=MT^{-3}\,\,\,\,\,\, \Longrightarrow \,\,\,\,\,\,\mathrm{unidad}\,\,\mathrm{SI}\,\,\mathrm{de}\,\, I = 1\,\mathrm{kg}\cdot\mathrm{s}^{-3}](/wiki/images/math/3/3/e/33ed3a44bf8034bfb6b44469d89288a9.png)
Pero es más frecuente expresar la unidad SI de la intensidad de una onda de este otro modo equivalente:
donde se ha tenido en cuenta que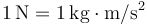 
, que 
, y que 
