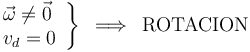No Boletín - Identificación de movimiento a partir de tres velocidades (Ex.Dic/12)

De Laplace

1 Enunciado

Las posiciones y velocidades instantáneas de tres puntos de un sólido rígido respecto a un sistema de referencia cartesiano 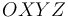$OXYZ\,$ vienen dadas por:

Punto	$\vec{r}$ (m)	$\vec{v}$ (m/s)
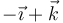
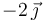
A	$-\vec{\imath}+\vec{k}$	$-2\,\vec{\jmath}$
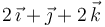
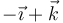
B	$2\,\vec{\imath}+\vec{\jmath}+2\,\vec{k}$	$-\vec{\imath}+\vec{k}$
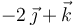
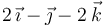
C	$-2\,\vec{\jmath}+\vec{k}$	$2\,\vec{\imath}-\vec{\jmath}-2\,\vec{k}$

¿Qué tipo de movimiento instantáneo es?

2 Solución

Deducimos, en primer lugar, el vector velocidad angular 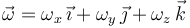$\,\vec{\omega}=\omega_x\,\vec{\imath}+\omega_y\,\vec{\jmath}+\omega_z\,\vec{k}\,\,$ del sólido, componente a componente, exigiendo el cumplimiento de la ecuación del campo de velocidades en la relación entre las velocidades conocidas.

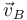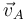Por ejemplo, la relación entre $\vec{v}_B\,$ y $\vec{v}_A\,$ debe satisfacer la ecuación:

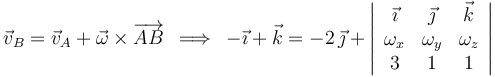
$\vec{v}_B=\vec{v}_A+\vec{\omega}\times\overrightarrow{AB}\,\,\,\Longrightarrow\,\,\,-\vec{\imath}+\vec{k}=-2\,\vec{\jmath}+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & \omega_y & \omega_z \\ 3 & 1 & 1 \end{array}\right|$

E igualando componentes homólogas:

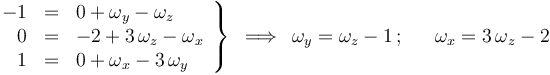
$\left.\begin{array}{rcl} -1 & = & 0+\omega_y-\omega_z \\ 0 & = & -2+3\,\omega_z-\omega_x \\ 1 & = & 0+\omega_x-3\,\omega_y \end{array}\right\}\,\,\,\Longrightarrow\,\,\, \omega_y=\omega_z-1\,;\,\,\,\,\,\,\,\,\,\omega_x=3\,\omega_z-2$

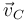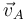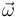Y relacionando de forma análoga $\vec{v}_C\,$ y $\vec{v}_A\,$ , podemos culminar la deducción de $\vec{\omega}\,$ :

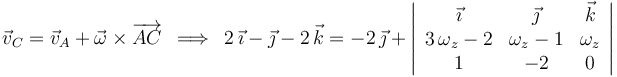
$\vec{v}_C=\vec{v}_A+\vec{\omega}\times\overrightarrow{AC}\,\,\,\Longrightarrow\,\,\,2\,\vec{\imath}-\vec{\jmath}-2\,\vec{k}=-2\,\vec{\jmath}+\left|\begin{array}{ccc} \vec{\imath} & \vec{\jmath} & \vec{k} \\ 3\,\omega_z-2 & \omega_z-1 & \omega_z \\ 1 & -2 & 0 \end{array}\right|$

E igualando componentes homólogas:

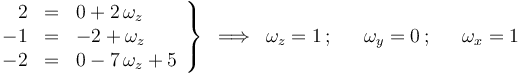
$\left.\begin{array}{rcl} 2 & = & 0+2\,\omega_z \\ -1 & = & -2+\omega_z \\ -2 & = & 0-7\,\omega_z+5 \end{array}\right\}\,\,\,\Longrightarrow\,\,\, \omega_z=1\,;\,\,\,\,\,\,\,\,\,\omega_y=0\,;\,\,\,\,\,\,\,\,\,\omega_x=1$

Por tanto, el vector velocidad angular es:

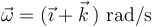
$\vec{\omega}=(\vec{\imath}+\vec{k}\,)\,\,\mathrm{rad/s}$

A continuación, calculamos la velocidad de deslizamiento 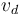$v_d\,$ , que es la proyección de la velocidad de cualquier punto sobre la velocidad angular:

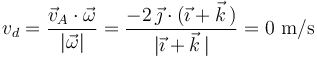
$v_d=\frac{\vec{v}_A\cdot\vec{\omega}}{|\vec{\omega}|}=\frac{-2\,\vec{\jmath}\cdot(\vec{\imath}+\vec{k}\,)}{|\vec{\imath}+\vec{k}\,|}=0\,\,\mathrm{m/s}$

Conocidos los invariantes primero (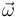 $\vec{\omega}\,$ ) y segundo ( 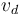$v_d\,$ ), procedemos a clasificar el movimiento instantáneo del sólido rígido:

$\left.\begin{array}{l} \vec{\omega}\neq\vec{0} \\ v_d=0 \end{array}\right\}\,\,\,\Longrightarrow\,\,\,\mathrm{ROTACION}$

No Boletín - Identificación de movimiento a partir de tres velocidades (Ex.Dic/12)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES