No Boletín - Guía ranurada horizontal y manivela (Ex.Sep/15)
De Laplace
Contenido |
1 Enunciado
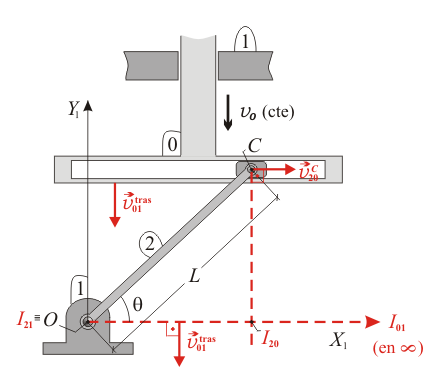
El plano fijo  (sólido "1") de la figura contiene en todo instante a dos sólidos en movimiento: una guía horizontal ranurada (sólido "0"), que se traslada verticalmente hacia abajo con celeridad constante
(sólido "1") de la figura contiene en todo instante a dos sólidos en movimiento: una guía horizontal ranurada (sólido "0"), que se traslada verticalmente hacia abajo con celeridad constante 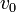 ; y la manivela
; y la manivela 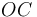 (sólido "2") de longitud
(sólido "2") de longitud  , que rota alrededor del eje fijo
, que rota alrededor del eje fijo 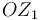 . Los movimientos de los sólidos "2" y "0" se hallan vinculados entre sí porque el extremo
. Los movimientos de los sólidos "2" y "0" se hallan vinculados entre sí porque el extremo  de la manivela está obligado a deslizar en todo instante a lo largo de la ranura de la guía.
de la manivela está obligado a deslizar en todo instante a lo largo de la ranura de la guía.
Utilizando el ángulo  definido en la figura como parámetro auxiliar descriptivo de la posición del sistema, se pide:
definido en la figura como parámetro auxiliar descriptivo de la posición del sistema, se pide:
- Determinación gráfica (razonada) de las posiciones de los centros instantáneos de rotación
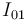 ,
,  e
e 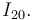
- Reducciones cinemáticas de los movimientos
 ,
,  y
y  en el punto
en el punto 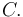
- Determinación de la velocidad
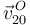 , las aceleraciones
, las aceleraciones 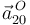 y
y 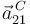 , y la aceleración angular
, y la aceleración angular 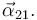
Aviso: Las magnitudes pedidas deben quedar expresadas en función de 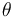 ,
, 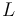 y/o
y/o 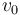 , pero NO en función de
, pero NO en función de 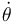 ni de
ni de 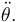
2 Determinación gráfica de los tres centros instantáneos de rotación
La manivela 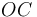 (sólido "2") se halla articulada en su extremo
(sólido "2") se halla articulada en su extremo  al origen de la escuadra fija
al origen de la escuadra fija  (sólido "1"). Por tanto, dicho punto
(sólido "1"). Por tanto, dicho punto  es un punto fijo (centro permanente de rotación) en el movimiento
es un punto fijo (centro permanente de rotación) en el movimiento  :
:
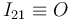
La guía horizontal ranurada (sólido "0") se traslada verticalmente respecto a la escuadra fija  (sólido "1"). En consecuencia, el centro instantáneo de rotación del movimiento
(sólido "1"). En consecuencia, el centro instantáneo de rotación del movimiento  se halla en el infinito en la dirección horizontal
(perpendicular a la dirección de traslación):
se halla en el infinito en la dirección horizontal
(perpendicular a la dirección de traslación):
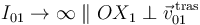
Dado que el extremo  de la manivela (sólido "2") está obligado a deslizar a lo largo de la ranura de la guía horizontal
(sólido "0"), la velocidad
de la manivela (sólido "2") está obligado a deslizar a lo largo de la ranura de la guía horizontal
(sólido "0"), la velocidad 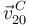 tiene necesariamente dirección paralela al eje
tiene necesariamente dirección paralela al eje 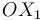 . Pues bien, tal como puede verse en la figura adjunta, el centro instantáneo de rotación
. Pues bien, tal como puede verse en la figura adjunta, el centro instantáneo de rotación 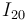 se halla en el punto donde se cortan la recta perpendicular a
se halla en el punto donde se cortan la recta perpendicular a 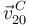 que pasa por
que pasa por  y la recta que pasa por
y la recta que pasa por  e
e 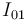 (esta última coincide con el eje
(esta última coincide con el eje 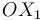 y se debe al teorema de los tres centros).
y se debe al teorema de los tres centros).
3 Determinación de las tres reducciones cinemáticas en el punto C
La reducción cinemática del movimiento  se deduce directamente del enunciado. Al ser
se deduce directamente del enunciado. Al ser  una traslación, la velocidad angular
una traslación, la velocidad angular 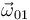 es nula, y la velocidad
es nula, y la velocidad 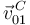 es la velocidad de dicha traslación:
es la velocidad de dicha traslación:

De la reducción cinemática del movimiento  , sabemos a priori la dirección de la velocidad angular
, sabemos a priori la dirección de la velocidad angular 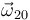 (perpendicular al plano director
(perpendicular al plano director  , como corresponde a un movimiento plano de rotación) y la dirección de la velocidad
, como corresponde a un movimiento plano de rotación) y la dirección de la velocidad 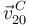 (horizontal como la guía, ya que el extremo
(horizontal como la guía, ya que el extremo  de la manivela se encuentra confinado en la ranura de la guía):
de la manivela se encuentra confinado en la ranura de la guía):

En cuanto a la reducción cinemática del movimiento  , también conocemos a priori la dirección de la velocidad angular
, también conocemos a priori la dirección de la velocidad angular
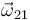 (perpendicular al plano director
(perpendicular al plano director  ), y podemos relacionar la velocidad
), y podemos relacionar la velocidad 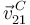 con
con 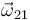 utilizando la ecuación del campo de velocidades
utilizando la ecuación del campo de velocidades
 y teniendo en cuenta que
y teniendo en cuenta que 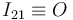 (por tanto,
(por tanto, 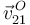 es nula):
es nula):
![\vec{\omega}_{21}=\omega_{21}\,\vec{k}_1\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\vec{v}^{\, C}_{21}=\underbrace{\vec{v}^{\, O}_{21}}_{=\,\vec{0}}+\,\,\vec{\omega}_{21}\,\times\,
\overrightarrow{OC}=\omega_{21}\,\vec{k}_1\,\times\, L\,[\,\mathrm{cos}(\theta)\,\vec{\imath}_1\,+\,\mathrm{sen}(\theta)\,\vec{\jmath}_1\,]=\omega_{21}L\,[-\mathrm{sen}(\theta)\,\vec{\imath}_1\,+\,\mathrm{cos}(\theta)\,\vec{\jmath}_1\,]](/wiki/images/math/d/c/8/dc8479b3fe918751ebad7c394c054652.png)
donde ![\overrightarrow{OC}=L\,[\,\mathrm{cos}(\theta)\,\vec{\imath}_1+\mathrm{sen}(\theta)\,\vec{\jmath}_1\,]\,](/wiki/images/math/4/4/d/44d3d150ab437bbd44741e26bb574970.png) se deduce por inspección de las razones trigonométricas en el triángulo rectángulo
se deduce por inspección de las razones trigonométricas en el triángulo rectángulo 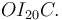
Planteadas las tres reducciones cinemáticas en  , se exige el cumplimiento de la ley de composición de velocidades angulares y de la ley de composición de velocidades, obteniéndose un sistema de tres ecuaciones para tres incógnitas:
, se exige el cumplimiento de la ley de composición de velocidades angulares y de la ley de composición de velocidades, obteniéndose un sistema de tres ecuaciones para tres incógnitas:
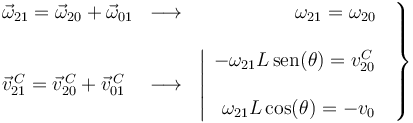
cuya solución es:
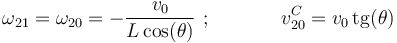
Y sustituyendo en las expresiones de las reducciones cinemáticas de los movimientos  y
y  , se obtiene:
, se obtiene:
![\vec{\omega}_{20}=-\displaystyle\frac{v_0}{L\,\mathrm{cos}(\theta)}\,\vec{k}_1\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\vec{v}^{\, C}_{20}=v_0\,\mathrm{tg}(\theta)\,\vec{\imath}_1\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\vec{\omega}_{21}=-\displaystyle\frac{v_0}{L\,\mathrm{cos}(\theta)}\,\vec{k}_1\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
\vec{v}^{\, C}_{21}=v_0\,[\,\mathrm{tg}(\theta)\,\vec{\imath}_1-\,\vec{\jmath}_1]](/wiki/images/math/c/e/e/ceec0049fc384c3f99585f0018aa0890.png)
4 Cálculo de las demás magnitudes cinemáticas solicitadas
La velocidad 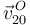 se puede deducir aplicando la ley de composición de velocidades en el punto
se puede deducir aplicando la ley de composición de velocidades en el punto  :
:

La aceleración 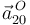 se puede deducir aplicando la ley de composición de aceleraciones en el punto
se puede deducir aplicando la ley de composición de aceleraciones en el punto  :
:

donde se ha tenido en cuenta que el punto  es un punto fijo en el movimiento
es un punto fijo en el movimiento  (por eso
(por eso 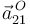 es nula), y que la traslación
es nula), y que la traslación  es de velocidad constante (por eso
es de velocidad constante (por eso 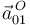 es nula).
es nula).
La aceleración angular 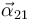 se puede obtener a partir de su definición:
se puede obtener a partir de su definición:
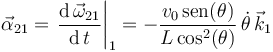
Pero el enunciado del problema nos dice que 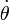 no debe aparecer en los resultados finales. Así que, teniendo en cuenta la definición del ángulo
no debe aparecer en los resultados finales. Así que, teniendo en cuenta la definición del ángulo  , relacionaremos
, relacionaremos 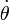 con la velocidad angular del movimiento
con la velocidad angular del movimiento  (ya determinada en el apartado anterior):
(ya determinada en el apartado anterior):

Y sustituyendo esta expresión de 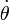 , completamos la determinación de la aceleración angular
, completamos la determinación de la aceleración angular 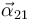 :
:
![\vec{\alpha}_{21}=
-\frac{v_0\,\mathrm{sen}(\theta)}{L\,\mathrm{cos}^2(\theta)}\left[-\frac{v_0}{L\,\mathrm{cos}(\theta)}\right]
\vec{k}_1=\displaystyle\frac{v_0^2\,\mathrm{sen}(\theta)}{L^2\,\mathrm{cos}^3(\theta)}\,\vec{k}_1](/wiki/images/math/0/0/9/009841d7f0bcf99fb6d4418af5029f9f.png)
Por último, la aceleración 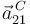 se puede obtener a partir de
se puede obtener a partir de 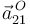 ,
, 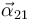 y
y 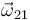 mediante la ecuación del campo de aceleraciones del movimiento
mediante la ecuación del campo de aceleraciones del movimiento  :
: