No Boletín - Fuerza neta sobre un vehículo en una curva (Ex.Sep/15)
De Laplace
1 Enunciado
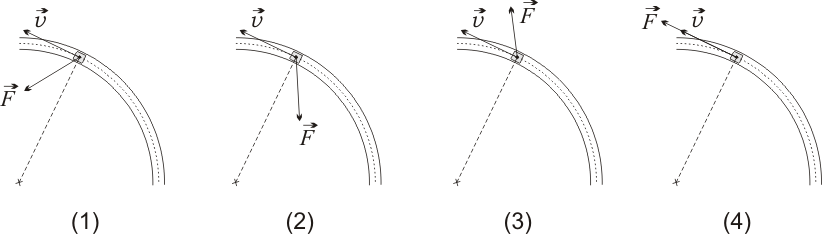
Un vehículo (masa  ) está saliendo de una curva, y su celeridad (
) está saliendo de una curva, y su celeridad ( ) está aumentando. ¿Cuál de los siguientes diagramas representa correctamente la dirección y el sentido de la fuerza neta (
) está aumentando. ¿Cuál de los siguientes diagramas representa correctamente la dirección y el sentido de la fuerza neta (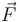 ) que actúa sobre dicho vehículo?
) que actúa sobre dicho vehículo?
2 Solución
Modelando el vehículo como una partícula de masa inercial constante 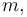 podemos asegurar que la fuerza neta
podemos asegurar que la fuerza neta 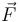 que actúa sobre el mismo es un vector con la misma dirección y el mismo sentido que su vector aceleración
que actúa sobre el mismo es un vector con la misma dirección y el mismo sentido que su vector aceleración  ya que la segunda ley de Newton establece que:
ya que la segunda ley de Newton establece que:
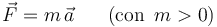
Pero el hecho de que 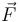 y
y 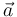 compartan la misma dirección y el mismo sentido reduce este ejercicio a una cuestión puramente cinemática: ¿qué sabemos sobre la orientación del vector
compartan la misma dirección y el mismo sentido reduce este ejercicio a una cuestión puramente cinemática: ¿qué sabemos sobre la orientación del vector 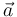 de un vehículo que describe una trayectoria curva y cuya celeridad está creciendo?
de un vehículo que describe una trayectoria curva y cuya celeridad está creciendo?
Pues bien, sabemos que la aceleración tangencial (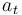 ) y la aceleración normal (
) y la aceleración normal (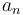 ) de tal vehículo son ambas estrictamente positivas:
) de tal vehículo son ambas estrictamente positivas:
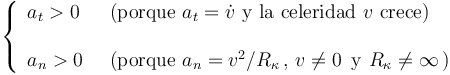
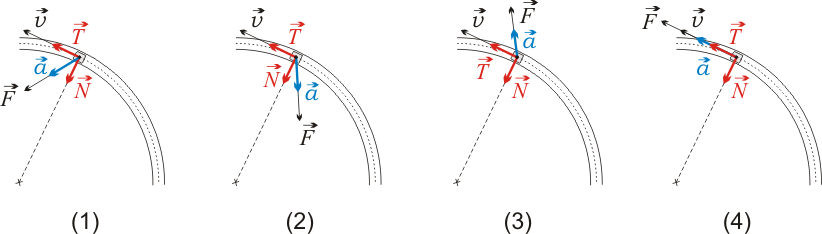
Para que el conocimiento de los signos de 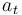 y
y 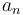 permita predecir la orientación correcta del vector
permita predecir la orientación correcta del vector 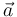 , es necesario determinar antes el vector tangente unitario
, es necesario determinar antes el vector tangente unitario 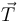 y el vector normal principal
y el vector normal principal 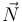 . En los diagramas propuestos, obtenemos
. En los diagramas propuestos, obtenemos 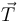 normalizando el vector velocidad
normalizando el vector velocidad 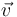 del vehículo, y
del vehículo, y 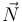 trazando el unitario que apunta desde el vehículo hacia el centro de curvatura (representado por una pequeña aspa):
trazando el unitario que apunta desde el vehículo hacia el centro de curvatura (representado por una pequeña aspa):
Que las componentes tangencial y normal de la aceleración del vehículo sean ambas estrictamente positivas (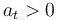 y
y 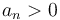 ) requiere que el vector aceleración
) requiere que el vector aceleración 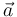 forme simultáneamente ángulos agudos con el vector tangente unitario
forme simultáneamente ángulos agudos con el vector tangente unitario 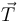 y con el vector normal principal
y con el vector normal principal 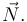
Analizando con este criterio los cuatro casos propuestos, llegamos a la conclusión de que el diagrama (1) es el correcto:
| Diagrama | Ángulo entre 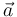 y y 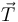
| Ángulo entre 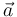 y y 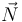
| |
|---|---|---|---|
| (1) | agudo (at > 0) | agudo (an > 0) | Correcto |
| (2) | obtuso (at < 0) | agudo (an > 0) | Incorrecto |
| (3) | agudo (at > 0) | obtuso (an < 0) | Incorrecto |
| (4) | nulo (at > 0) | recto (an = 0) | Incorrecto |