No Boletín - Ecuaciones horarias en coordenadas polares (Ex.Jun/13)
De Laplace
Contenido |
1 Enunciado
El movimiento de una partícula  , de masa
, de masa 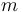 , en el plano
, en el plano 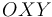 queda descrito en coordenadas polares mediante las ecuaciones horarias:
queda descrito en coordenadas polares mediante las ecuaciones horarias:

siendo 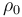 ,
, 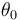 ,
, 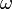 y
y 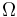 constantes conocidas.
constantes conocidas.
- Evalúe la energía cinética de la partícula
 en el instante inicial
en el instante inicial 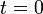 .
.
- Determine (en función del tiempo) la aceleración de la partícula
 en componentes polares.
en componentes polares.
- Determine (en función del tiempo) el momento cinético de la partícula
 respecto al origen de coordenadas
respecto al origen de coordenadas  .
.
- Deduzca razonadamente la relación que debe existir entre las constantes
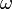 y
y 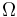 para que el movimiento de la partícula
para que el movimiento de la partícula  sea un movimiento central con centro en
sea un movimiento central con centro en  .
.
2 Energía cinética en el instante inicial
La velocidad de la partícula  en componentes polares viene dada por la expresión:
en componentes polares viene dada por la expresión:
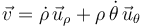
Calculando las primeras derivadas respecto al tiempo de las ecuaciones horarias, y sustituyéndolas después en dicha expresión, se obtiene:
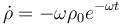 ;
; 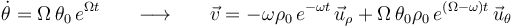
Haciendo el producto escalar del vector velocidad por sí mismo, obtenemos el cuadrado de la celeridad:
![v^2 = \vec{v}\cdot\vec{v} = \rho_0^2\left[\omega^2 e^{-2\omega t}+\Omega^2\theta_0^2\,e^{2(\Omega-\omega) t}\right]](/wiki/images/math/8/e/7/8e71f6e4bed62708d7b18e6bf0bd8393.png)
que, evaluado en el instante inicial 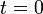 y multiplicado por el factor
y multiplicado por el factor 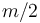 , nos da la energía cinética inicial de la partícula
, nos da la energía cinética inicial de la partícula  :
:
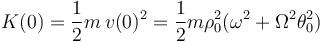
3 Aceleración en componentes polares
La aceleración de la partícula  en componentes polares viene dada por la expresión:
en componentes polares viene dada por la expresión:
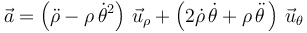
Calculando las segundas derivadas respecto al tiempo de las ecuaciones horarias, y sustituyendo después en la expresión de la aceleración tanto éstas como las derivadas primeras anteriormente determinadas, se obtiene:
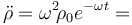 ;
; 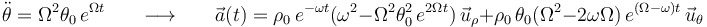
4 Momento cinético respecto al origen de coordenadas
El momento cinético de la partícula  respecto al origen de coordenadas
respecto al origen de coordenadas  se define como:
se define como:
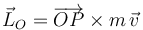
Sustituyendo 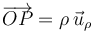 y
y 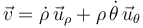 en la anterior expresión, se obtiene:
en la anterior expresión, se obtiene:
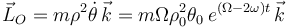
5 Movimiento central con centro en el origen de coordenadas
Si el movimiento de la partícula  es un movimiento central con centro en el punto
es un movimiento central con centro en el punto  , su momento cinético respecto a dicho punto ha de ser constante (independiente del tiempo). Que la expresión de
, su momento cinético respecto a dicho punto ha de ser constante (independiente del tiempo). Que la expresión de 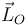 obtenida en el apartado anterior cumpla esta condición exige la nulidad del coeficiente que multiplica al tiempo en la exponencial, y de ahí se deduce la relación necesaria entre
obtenida en el apartado anterior cumpla esta condición exige la nulidad del coeficiente que multiplica al tiempo en la exponencial, y de ahí se deduce la relación necesaria entre 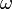 y
y 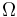 :
: