No Boletín - Dos partículas con distancia mutua constante II (Ex.Feb/17)

De Laplace

1 Enunciado

Las partículas $A\,$ y $B\,$ se mueven a lo largo de los ejes $OX\,$ y $OY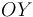\,$ , respectivamente, en los sentidos de avance que se indican en la figura, y de tal modo que su distancia mutua permanece constante en el tiempo:

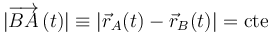
$|\overrightarrow{BA}\,(t)|\equiv|\vec{r}_A(t)-\vec{r}_B(t)|=\mathrm{cte}$

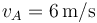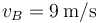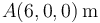En cierto instante, las celeridades de las partículas son $v_A=6\,\mathrm{m}\mathrm{/}\mathrm{s}\,$ y $v_B=9\,\mathrm{m}\mathrm{/}\mathrm{s}\,$ , respectivamente, y la posición de la primera partícula es $A(6,0,0)\,\mathrm{m}\,$ .

¿Cuál es la posición de la segunda partícula en dicho instante?

2 Solución

Dos partículas obligadas a mantener su distancia mutua constante a lo largo del tiempo constituyen el sólido rígido más simple de todos los posibles. Y, por tanto, sus velocidades habrán de satisfacer permanentemente la condición de equiproyectividad:

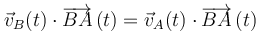
$\vec{v}_{B}(t)\cdot\overrightarrow{BA}\,(t)=\vec{v}_{A}(t)\cdot\overrightarrow{BA}\,(t)$

Particularizando esta condición para el instante considerado en el enunciado, vamos a ser capaces de responder la pregunta planteada.

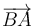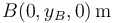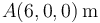El vector $\overrightarrow{BA}\,$ se calcula restándole las coordenadas del punto $B(0,y_B,0)\,\mathrm{m}\,$ a las coordenadas del punto $A(6,0,0)\,\mathrm{m}\,$ :

$\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}=(6\,\vec{\imath}-y_B\,\vec{\jmath}\,)\,\,\mathrm{m}$

donde 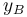$y_B\,$ es la incógnita a determinar.

Por otra parte, conocemos las velocidades de ambas partículas en el instantes de interés:

$\vec{v}_{A}=6\,\vec{\imath}\,\,\,\mathrm{m}\mathrm{/}\mathrm{s}\,\,;\,\,\,\,\,\,\,\,\,\vec{v}_{B}=-\,9\,\vec{\jmath}\,\,\,\mathrm{m}\mathrm{/}\mathrm{s}$

Exigiendo la equiproyectividad de velocidades en dicho instante, comprobamos que se puede obtener fácilmente la posición del punto $B\,$ :

$\vec{v}_{B}\,\cdot\,\overrightarrow{BA}=\vec{v}_{A}\,\cdot\,\overrightarrow{BA}\,\,\,\,\,\Longrightarrow\,\,\,\,\, -\,9\,\vec{\jmath}\,\,\cdot\,(6\,\vec{\imath}\,-\,y_B\,\vec{\jmath}\,)=6\,\vec{\imath}\,\,\cdot\,(6\,\vec{\imath}\,-\,y_B\,\vec{\jmath}\,) \,\,\,\,\,\Longrightarrow\,\,\,\,\, 9\,y_B=36\,\,\,\,\,\Longrightarrow\,\,\,\,\,y_B=4\,\mathrm{m}\,\,\,\,\,\longrightarrow\,\,\,\,\, B(0,4,0)\,\mathrm{m}$

No Boletín - Dos partículas con distancia mutua constante II (Ex.Feb/17)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES