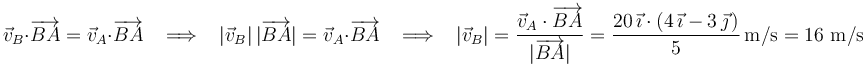No Boletín - Dos partículas con distancia mutua constante (Ex.Jun/13)
De Laplace
1 Enunciado
Las partículas  y
y  se mueven en el plano
se mueven en el plano  de tal modo que su distancia mutua permanece constante a lo largo del tiempo:
de tal modo que su distancia mutua permanece constante a lo largo del tiempo:
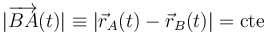
Además,  persigue a
persigue a  , es decir, el vector velocidad
, es decir, el vector velocidad 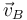 tiene siempre la misma dirección que la recta imaginaria que pasa por
tiene siempre la misma dirección que la recta imaginaria que pasa por  y
y  . En cierto instante, las posiciones de ambas partículas son
. En cierto instante, las posiciones de ambas partículas son 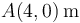 y
y 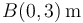 , y la velocidad de
, y la velocidad de  es
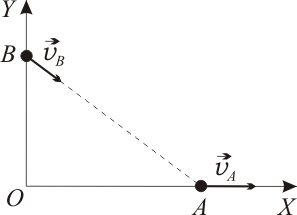
es 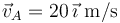 (ver figura).
(ver figura).
¿Cuánto vale la celeridad de  en dicho instante?
en dicho instante?
2 Solución
Dos partículas obligadas a mantener su distancia mutua constante a lo largo del tiempo constituyen el sólido rígido más simple de todos los posibles. Y, por tanto, sus velocidades habrán de satisfacer permanentemente la condición de equiproyectividad:
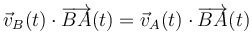
Particularizando esta condición para el instante considerado en el enunciado, vamos a ser capaces de responder la pregunta planteada.
El vector 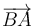 se calcula restándole las coordenadas del punto
se calcula restándole las coordenadas del punto  a las coordenadas del punto
a las coordenadas del punto  :
:
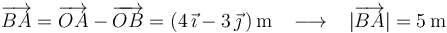
Por otra parte, sabemos que la velocidad  tiene la misma dirección y el mismo sentido que el vector
tiene la misma dirección y el mismo sentido que el vector 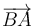 (porque
(porque  persigue a
persigue a  ), lo cual nos permite identificar el producto escalar de estos dos vectores con el producto de sus respectivos módulos.
), lo cual nos permite identificar el producto escalar de estos dos vectores con el producto de sus respectivos módulos.
Teniendo esto en cuenta y exigiendo la equiproyectividad de velocidades en el instante de interés, comprobamos que se puede obtener fácilmente la celeridad del punto  en dicho instante:
en dicho instante: